Arithmetic combinator: Difference between revisions
| Line 62: | Line 62: | ||
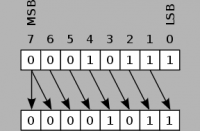
If shifting right and the number is positive (MSB=0), a 0 is inserted into the MSB and the bit in the LSB is lost. | If shifting right and the number is positive (MSB=0), a 0 is inserted into the MSB and the bit in the LSB is lost. | ||
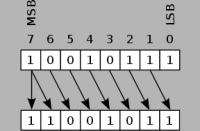
If shifting right and the number is negative (MSB=1), a 1 is inserted into the MSB to keep the sign and the bit in the LSB is lost. | If shifting right and the number is negative (MSB=1), a 1 is inserted into the MSB to keep the sign and the bit in the LSB is lost. | ||
[[File:Bitshiftleft.png|none|thumb|200px|Example of a 'bit shift left'.]] [[File:BitshiftRightZero.png|none|thumb|200px|Example of a 'bit shift right (positive number)'.]] [[File:BitshiftRightOne.png|none|thumb|200px|Example of a 'bit shift | [[File:Bitshiftleft.png|none|thumb|200px|Example of a 'bit shift left'.]] [[File:BitshiftRightZero.png|none|thumb|200px|Example of a 'bit shift right (positive number)'.]] [[File:BitshiftRightOne.png|none|thumb|200px|Example of a 'bit shift right (negative number)'.]] | ||
== History == | == History == | ||
Revision as of 10:18, 29 September 2024
| Arithmetic combinator |
|
Recipe |
|||||||||||||
| ++ → | |||||||||||||
|
Total raw |
|||||||||||||
| ++ | |||||||||||||
|
Map color |
|||||||||||||
|
Health |
|
||||||||||||
|
Stack size |
50 |
||||||||||||
|
50 (1 stack) |
|||||||||||||
|
Energy consumption |
1 kw (electric) |
||||||||||||
|
Mining time |
0.1 |
||||||||||||
|
Prototype type |
|||||||||||||
|
Internal name |
arithmetic-combinator |
||||||||||||
|
Required technologies |
|||||||||||||
|
Produced by |
|||||||||||||
The arithmetic combinator is part of the circuit network and one of three types of combinators available in the game (along with the constant combinator and decider combinator). Each arithmetic combinator can perform any one of the following mathematical operations on signals, and will show the corresponding symbol on its top:
- addition (+)
- subtraction (−)
- multiplication (*)
- division (/)
- modulo (%)
- exponentiation (^)
- bit shift left (<<)
- bit shift right (>>)
- bitwise AND (&)
- bitwise OR (|)
- bitwise XOR (^)
The arithmetic combinator accepts two input connections (red and green wires), and sends its output to both output connections. The input wires connect to the nubs on the left side of the sprite in the sidebar, while the outputs connect to the right side.
Function
The internal logic process has three steps:
- All input signals on the red and green wires are summed within the combinator.
- The specified operation is performed on the selected signal(s).
- The result of this operation is output as the selected output signal.
The operands can be any single signal or a constant value. Up to one of the operands can be the each virtual signal.
If neither operand is the each signal, the output must be a single signal. The operation is performed on the values of the chosen left and right signals, and the result is sent to the output on the specified signal.
If one operand is the each signal, then the output can be a single signal or the each signal. If the output is the each signal, then the operation is performed individually on the value of each input signal along with the value of the other operand, and each result is sent to the output on the same signal. If the output is a single signal, the operation is done on each of the input signals, the individual results are all added together, and that result is sent to the output on the specified signal.
Notes on operations
When using division, the result is truncated:
- 21 / 10 = 2
- 19 / 10 = 1
- −21 / 10 = −2
- −19 / 10 = −1
- 21 / −10 = −2
- 19 / −10 = −1
- −21 / −10 = 2
- −19 / −10 = 1
Modulo, indicated using % as it is in most programming languages, is the remainder after division. For example, 13 % 3 is 1 (13 = 4 * 3 + 1). This can, for example, be combined with truncated division as described above to separate out individual digits of a number for use in building visual indicators:
- (24321 / 10000) % 10 = 2
- (24321 / 1000) % 10 = 4
- (24321 / 100) % 10 = 3
- (24321 / 10) % 10 = 2
- (24321 / 1) % 10 = 1
Negating the left operand of a modulo negates the result, while negating the right operand does nothing:
- 13 % 3 = 1
- 13 % −3 = 1
- −13 % 3 = −1
- −13 % −3 = −1
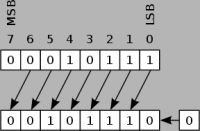
Bit shift right and Bit shift left deal with numbers in the binary representation. The 0's and 1's that make up a number are shifted in the specified direction which can result in a completely different number, due to the change in the binary value. The shift performed is called arithmetic shift, because it preserves the sign bit on bit shift right. If shifting left, a 0 is inserted into the least significant bit (LSB), and the bit in the most significant bit (MSB) is lost. If shifting right and the number is positive (MSB=0), a 0 is inserted into the MSB and the bit in the LSB is lost. If shifting right and the number is negative (MSB=1), a 1 is inserted into the MSB to keep the sign and the bit in the LSB is lost.
History
- 0.15.0:
- Added Modulo, Power, Left Bit Shift, Right Bit Shift, Bitwise AND, Bitwise OR and Bitwise XOR to the Arithmetic Combinator.
- 0.13.0:
- Connected wires are highlighted when hovering over a combinator connected to the circuit network.
- Combinators show input and output in alt mode.
- More virtual signals for combinators.
- Constant combinator can be rotated.
- Decider combinator "input count" option makes the combinator copy the count of the specified output signal from the input signals, instead of copying the count from the condition.
- New combinator graphics.
- 0.12.5:
- Combinators now emit light.
- 0.12.2:
- Combinators no longer turn off when no wires are connected.
- 0.12.0:
- Introduced