|
|
| (15 intermediate revisions by 4 users not shown) |
| Line 2: |
Line 2: |
|
| |
|
| '''Uranium processing''' is the only way to use [[uranium ore]] and the first source of [[uranium-235]] and [[uranium-238]] that is available to the [[player]]. The process has a 99.3% chance to produce 1 uranium-238 and a 0.7% chance to produce 1 uranium-235. | | '''Uranium processing''' is the only way to use [[uranium ore]] and the first source of [[uranium-235]] and [[uranium-238]] that is available to the [[player]]. The process has a 99.3% chance to produce 1 uranium-238 and a 0.7% chance to produce 1 uranium-235. |
| | |
|
| |
|
| == Initiating the [[Kovarex enrichment process]] == | | == Initiating the [[Kovarex enrichment process]] == |
| Unlike all other crafting processes in the game, uranium processing creates U-235 and U-238 based on probability, rather than in guaranteed deterministic amounts. Additionally, the Kovarex process requires a bulk stockpile of 40 units of the rare uranium-235 isotope to initiate in a single centrifuge. Therefore, planning uranium mining and processing for the Kovarex process takes certain considerations not encountered elsewhere in the game. | | Unlike most other crafting processes, uranium processing creates U-235 and U-238 based on probability, rather than in guaranteed deterministic amounts. Additionally, the Kovarex process requires a bulk stockpile of 40 units of the rare uranium-235 isotope to initiate in a single centrifuge. Therefore, planning uranium mining and processing for the Kovarex process takes certain considerations not encountered elsewhere in the game. |
|
| |
|
| === Expected value === | | === Expected value === |
| Line 10: |
Line 11: |
|
| |
|
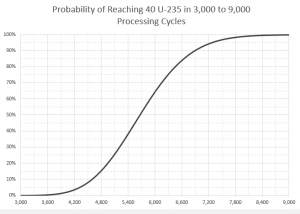
| However, given the nature of probability, it is impossible to guarantee that 40 units will be reached in this number of cycles; as a matter of fact, some mathematics yields that the probability that 5,714 cycles will produce ''at least'' 40 units of U-235 is only about 52%. | | However, given the nature of probability, it is impossible to guarantee that 40 units will be reached in this number of cycles; as a matter of fact, some mathematics yields that the probability that 5,714 cycles will produce ''at least'' 40 units of U-235 is only about 52%. |
| | |
| | As each cycle takes 12 seconds, it takes on average 12 * 143 = 1716 seconds to produce 1 U-235 (assuming no productivity or speed modules). This can be turned into 10 [[uranium fuel cell|uranium fuel cells]], each of which lasts 200 seconds, so in total 2000 seconds. That means one centrifuge constantly running can produce enough fuel cells to continuously power one reactor, although this is random. See [[Tutorial:Nuclear_power#Nuclear_reactor]]. The Kovarex enrichment process is a much more efficient way to produce U-235. |
|
| |
|
| === Confidence levels === | | === Confidence levels === |
| Line 37: |
Line 40: |
| |} | | |} |
|
| |
|
| == Precise Mathematical Analysis == | | == Trivia == |
| To determine the exact number of [[centrifuge]]s required for maintaining [[reactor]] stability without using the [[Kovarex enrichment process]], we need to employ probability theory. This analysis will help us estimate the probability of obtaining the required amount of [[uranium-235]] and the number of [[centrifuge]]s needed.
| | * Excluding Space Age-exclusive recipes, this is the only recipe in the base game to have random products. |
| | |
| The primary goal of these calculations is to derive a formula that can be easily applied and sustainable for predictions despite advancements in [[technologies]], game version updates, or in-game developments and modifications.
| |
| | |
| === Variables ===
| |
| Let's introduce some variables that we'll need in further calculations
| |
| | |
| * ''<code>T</code> - overall time of a [[reactor]] working (in seconds*)''
| |
| * ''<code>t</code> - time of a [[reactor]] cycle (in seconds*)''
| |
| * ''<code>c</code> - consumption of [[uranium-235]] per reactor cycle'' | |
| * ''<code>k</code> - [[centrifuge]]s number (our target value for calculations)''
| |
| * ''<code>p</code> - probability of [[uranium-235]] production per centrifuge cycle''
| |
| * ''<code>n</code> - overall number of [[centrifuge]] cycles''
| |
| * ''<code>τ</code> - [[centrifuge]] time per cycle''
| |
| * ''<code>α</code> - desired probability of having success number [[uranium-235]] to sustain all <code>T</code> time of [[reactor]] stable work**''
| |
| | |
| <nowiki>*</nowiki> Measured in seconds or in-game [[tick]]s, this does not affect the general reasoning
| |
| | |
| <nowiki>**</nowiki> Known as the [[https://en.wikipedia.org/wiki/Confidence_interval confidence level]]. Due to the nature of probability, this value can only be in the interval <code>(0; 1)</code>. We will use the values 0.9, 0.95, and 0.99 to maintain scientific rigor and ease of interpretation, opposite to the [[https://en.wikipedia.org/wiki/Statistical_significance significance level]].
| |
| | |
| === Assumptions ===
| |
| ;Assumption 1
| |
| : All <code>k</code> centrifuges work continuously and simultaneously for each <code>n</code> cycle with the same <code>τ</code>
| |
| ;Assumption 2
| |
| : There are always enough resources to convert [[uranium-235]] into reactor fuel *
| |
| ;Assumption 3
| |
| : The conversion of [[uranium-235]] into fuel for reactors can be neglected **
| |
| ;Assumption 4 (for long-term play)
| |
| : The game can be played indefinitely (technically assumed for practical use, average playtime suffices)
| |
| | |
| <nowiki>*</nowiki> For instance, base game [[uranium-238]] has a very high probability (<code>0.993</code>), ensuring a sufficient supply for [[uranium fuel cell]] production.
| |
| | |
| <nowiki>**</nowiki> For instance, converting base game [[uranium-235]] into 10 [[uranium fuel cell]]s takes <code>12 sec</code>, but the [[reactor]] cycle is <code>200 sec</code> - a negligible time difference, easily managed by building more [[assembler]]s.
| |
| | |
| === Exact Approach ===
| |
| The main question we aim to answer:
| |
| | |
| <blockquote>
| |
| How many <code>k</code> [[centrifuge]]s are needed during <code>n</code> cycles of [[centrifuge]] production to sustain a [[reactor]] working continuously for <code>T</code> time with probability <code>α</code>?
| |
| </blockquote>
| |
| Assume each [[centrifuge]] in each production cycle is represented by a discrete random variable '''''X<sub>ij</sub>''''', where '''''i''''' is the [[centrifuge]] number and '''''j''''' is the production cycle number. If '''''X<sub>ij</sub>''''' produces [[uranium-235]], its value is <code>X<sub>ij</sub>=1</code>. If not, <code>X<sub>ij</sub>=0</code>. Thus, <code> P(X<sub>ij</sub> = 1) = 0.007</code> and <code> P(X<sub>ij</sub> = 0) = 0.993</code> (This is a [[https://en.wikipedia.org/wiki/Bernoulli_distribution Bernoulli distribution]]).
| |
| | |
| To find out how long [[centrifuge]]s should produce [[uranium-235]] to sustain a [[reactor]]:
| |
| From one side, the [[reactor]] has <code>T/t</code> working cycles, needing a total of <code>Tc/t</code> [[uranium-235]] to run continuously for time '''''T'''''. Let's denote this value as '''''u''''': <code>u=Tc/t</code>.
| |
| From the other side, the [[centrifuge]]s work continuously for '''''n''''' cycles during time '''''T''''': <code>T = n*τ</code>.
| |
| | |
| Combining these, our required quantity of '''''u''''' is <code>u=n*τ*c/t</code> for the entire [[reactor]] operation time '''''T'''''.
| |
| | |
| Consider the simple case where we need '''''n''''' cycles and '''''k''''' [[centrifuge]]s to produce exactly '''''u''''' [[uranium-235]]. Each '''''X<sub>ij</sub>''''' is a Bernoulli trial, so <code>X<sub>all</sub> = ∑<sub>i</sub><sup>n</sup>∑<sub>j</sub><sup>k</sup>X<sub>ij</sub></code> is the total production, distributed as a [[https://en.wikipedia.org/wiki/Binomial_distribution binomial distribution]] <code>X<sub>all</sub> ~ B(nk, p)</code>. This gives the probability of producing exactly '''''u''''' [[uranium-235]] in '''''n''''' cycles with '''''k''''' [[centrifuge]]s:
| |
| <blockquote>
| |
| <code>P(X<sub>all</sub>=u) = C<sub>nk</sub><sup>u</sup> * p<sup>u</sup> * (1-p)<sup>nk-u</sup></code>
| |
| </blockquote>
| |
| Practically, we are interested in producing at least '''''u''''' [[uranium-235]], corresponding to <code>P(X<sub>all</sub> ≥ u)</code>. This can be calculated as <code>P(X<sub>all</sub> ≥ u) = 1 - P(X<sub>all</sub> < u)</code>, where <code>P(X<sub>all</sub> < u)</code> is the [[https://en.wikipedia.org/wiki/Binomial_distribution#:~=0.059535.-,Cumulative%20distribution%20function,-%5Bedit%5D cumulative distribution function]]:
| |
| <blockquote>
| |
| <code>P(X<sub>all</sub>≥u) ≥ α</code> ⇒ <code>1 - ∑<sub>m</sub><sup>u-1</sup>P(X<sub>all</sub>=m) ≥ α</code> ⇒ {using results from paragraph 1} ⇒ <code>∑<sub>m</sub><sup>n*τ*c/t-1</sup>C<sub>nk</sub><sup>m</sup> * p<sup>m</sup> * (1-p)<sup>nk-m</sup> ≤ 1 - α</code>
| |
| </blockquote>
| |
| So, we now have a formula to determine the number of '''''k''''' [[centrifuge]]s needed to sustain a [[reactor]] with consumption '''''c''''' during '''''n''''' cycles. This formula is general and not always practical for long-term play due to the high values of '''''n''''' and '''''u'''''. It is best suited for short-term or speedrun calculations.
| |
| | |
| ==== Example Base Game Short-Term ====
| |
| To illustrate, let's determine how many [[centrifuge]]s are needed to sustain 1 [[reactor]] with 0.99 confidence without modules. It's a common mistake to think that 0.007 is the production speed, but it represents the probability of producing [[uranium-235]] per cycle. Suppose we want a reactor to work for 2000 [[centrifuge]] production cycles (about 6.7 hours of reactor operation) with 1 [[centrifuge]]:
| |
| | |
| {| class="wikitable"
| |
| ! n !! tau !! c !! t !! m !! p !! u !! ceil(u-1) !! alpha !! 1-alpha !! !! k !! C(nk, m) !! P(m) !! ∑<sub>m</sub>P
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 0 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1 || 7,92E-07 || 7,92E-07
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 1 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2000 || 1,12E-05 || 1,20E-05
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 2 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,0E+06 || 7,86E-05 || 9,06E-05
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 3 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1,3E+09 || 0,0004 || 0,0005
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 4 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 6,6E+11 || 0,0013 || 0,0018
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 5 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,7E+14 || 0,0037 || 0,0054
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 6 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 8,8E+16 || 0,0086 || 0,0140
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 7 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,5E+19 || 0,0172 || 0,0312
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 8 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 6,3E+21 || 0,0302 || 0,0302
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 9 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1,4E+24 || 0,0472 || 0,0472
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 10 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,8E+26 || 0,0662 || 0,1133
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 11 || 0,007 || 12 || 11 || 0,99 || <span style="color: red">0,01</span> || || 1 || 5,0E+28 || 0,0844 || <span style="color: red">0,1977</span>
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 12 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 8,3E+30 || 0,0986 ||
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 13 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1,3E+33 || 0,1063 ||
| |
| |}
| |
| | |
| As you can see, we need to produce 12 '''''u''''' for 2000 cycles. According to our formula, we need to sum up all the probabilities of producing less than 12 [[uranium-235]] and compare this with our desired confidence level:
| |
| | |
| <code>∑<sub>m</sub><sup>2000120.1/200-1</sup>C<sub>20001</sub><sup>m</sup> * 0.007<sup>m</sup> * (1-0.007)<sup>20001-m</sup> = 7.92E-07 + 1.12E-05 + 7.86E-05 + 0.0004 + 0.0013 + 0.0037 + 0.0086 + 0.0172 + 0.0302 + 0.0472 + 0.0662 + 0.0844 = 0.1977</code>
| |
| | |
| We can interpret this value as the "Probability of producing less than the required amount of [[uranium-235]] for 2000 [[centrifuge]] cycles." This probability should be less than <code>1-α = 0.01</code>. However, since it is not, we cannot be sure that 1 [[centrifuge]] will produce enough [[uranium-235]] to sustain [[reactor]] operation during 2000 cycles. Therefore, we need to increase the number of [[centrifuge]]s.
| |
| | |
| {| class="wikitable"
| |
| ! n !! tau !! c !! t !! m !! p !! u !! ceil(u-1) !! alpha !! 1-alpha !! !! k !! C(nk, m) !! P(x=m) !! sum(P(m<=ceil(u-1)))
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 0 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1 || 6,3E-13 || 6,27E-13
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 1 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 4000 || 1,8E-11 || 1,83E-11
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 2 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 8,0E+06 || 2,5E-10 || 2,67E-10
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 3 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,1E+10 || 2,3E-09 || 2,61E-09
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 4 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,1E+13 || 1,6E-08 || 1,91E-08
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 5 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 8,5E+15 || 9,3E-08 || 1,12E-07
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 6 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 5,7E+18 || 4,4E-07 || 5,48E-07
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 7 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 3,2E+21 || 1,8E-06 || 2,30E-06
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 8 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,6E+24 || 6,2E-06 || 6,17E-06
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 9 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 7,2E+26 || 1,9E-05 || 1,93E-05
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 10 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 2,9E+29 || 0,0001 || 0,0001
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 11 || 0,007 || 12 || 11 || 0,99 || <span style="color: red">0,01</span> || || 2 || 1,0E+32 || 0,0001 || <span style="color: red">0,0002</span>
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 12 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 3,4E+34 || 0,0003 ||
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 13 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,1E+37 || 0,0007 ||
| |
| |}
| |
| | |
| And now you can see that our condition is fulfilled. Therefore, we can say that without any [[module]]s or [[Kovarex enrichment process]], we can achieve the stability of 1 [[reactor]] during 2000 [[centrifuge]] cycles using at least 2 [[centrifuge]]s! However, does this imply that we need 4 [[centrifuge]]s for 2 [[reactor]]s, 6 [[centrifuge]]s for 3 [[reactor]]s, and so on? I encourage you to think about this question yourself. You may be surprised by the results when applying the approach outlined above.
| |
| | |
| === Distribution Approximation ===
| |
| If you plan to play for an extended period while your [[reactor]] setup is operating, we can consider <code>n→∞</code>. In this case, since our [[centrifuge]]s' overall production <code>X<sub>all</sub> ~ B(nk, p)</code>, we can use the [[https://en.wikipedia.org/wiki/De_Moivre%E2%80%93Laplace_theorem De Moivre-Laplace theorem]]. In short, it states that if our random variable follows a binomial distribution with a large number of trials, then <code>(X<sub>all</sub>-nkp)/sqrt(nkp(1-p)) ~ N(0, 1)</code>. Thus, to estimate <code>P(X<sub>all</sub> ≥ u)</code>, we simplify it to:
| |
| | |
| <code>P((X<sub>all</sub>-nkp)/sqrt(nkp(1-p))) ≥ (u-nkp)/sqrt(nkp(1-p)) ≥ α</code> ⇒ <code>{1-P<sub>dist</sub> ≥ α}</code> ⇒ <code>(nkp - u)/sqrt(nkp(1-p)) ≥ ɸ<sup>-1</sup>(1-α)</code>, where ɸ<sup>-1</sup> is the inverse standard normal distribution, found using the [[https://en.wikipedia.org/wiki/Standard_normal_table standard normal table]].
| |
| | |
| Let's denote <code>ɸ<sup>-1</sup>(α)</code> as λ. For each confidence level α, we can calculate it from the standard normal table:
| |
| <code>λ<sub>0.99</sub>=2.3263</code>, <code>λ<sub>0.95</sub>=1.6449</code>, <code>λ<sub>0.9</sub>=1.2816</code>.
| |
| | |
| Now we need to solve the equation above for the variable '''''k''''':
| |
| | |
| <code>(nkp-u)/sqrt(nkp(1-p)) ≥ λ</code> ⇒ <code>(nkp-nτc/t)/sqrt(nkp(1-p)) ≥ λ</code>.
| |
| | |
| After some basic arithmetic operations and solving the quadratic equation, you can determine the value of '''''k''''':
| |
| | |
| <blockquote>
| |
| <code>k ≥ (χ<sub>1</sub> + sqrt(χ<sub>1</sub><sup>2</sup> + 4χ<sub>0</sub>χ<sub>2</sub>))/(2*χ<sub>0</sub>)</code>
| |
| where
| |
| <code>χ<sub>0</sub> = np</code>,
| |
| <code>χ<sub>1</sub> = λ*sqrt(np(1-p))</code>,
| |
| <code>χ<sub>2</sub> = nτc/t</code>,
| |
| <code>λ</code> is the inverse standard normal distribution (popular values: 2.3263; 1.6449; 1.2816 for corresponding α values: 0.99; 0.95; 0.9).
| |
| </blockquote>
| |
|
| |
|
| == History == | | == History == |
