|
|
| Line 37: |
Line 37: |
| |} | | |} |
|
| |
|
| == Precise Mathematical Analysis ==
| |
| To determine the exact number of [[centrifuge]]s required for maintaining [[reactor]] stability without using the [[Kovarex enrichment process]], we need to employ probability theory. This analysis will help us estimate the probability of obtaining the required amount of [[uranium-235]] and the number of [[centrifuge]]s needed.
| |
|
| |
| The primary goal of these calculations is to derive a formula that can be easily applied and sustainable for predictions despite advancements in [[technologies]], game version updates, or in-game developments and modifications.
| |
|
| |
| === Variables ===
| |
| Let's introduce some variables that we'll need in further calculations
| |
|
| |
| * ''<code>T</code> - overall time of a [[reactor]] working (in seconds*)''
| |
| * ''<code>t</code> - time of a [[reactor]] cycle (in seconds*)''
| |
| * ''<code>c</code> - consumption of [[uranium-235]] per reactor cycle''
| |
| * ''<code>k</code> - [[centrifuge]]s number (our target value for calculations)''
| |
| * ''<code>p</code> - probability of [[uranium-235]] production per centrifuge cycle''
| |
| * ''<code>n</code> - overall number of [[centrifuge]] cycles''
| |
| * ''<code>τ</code> - [[centrifuge]] time per cycle to produce 1 recipe''
| |
| * ''<code>α</code> - desired probability of having success number [[uranium-235]] to sustain all <code>T</code> time of [[reactor]] stable work**''
| |
|
| |
| <nowiki>*</nowiki> Measured in seconds or in-game [[tick]]s, this does not affect the general reasoning
| |
|
| |
| <nowiki>**</nowiki> Known as the [[https://en.wikipedia.org/wiki/Confidence_interval confidence level]]. Due to the nature of probability, this value can only be in the interval <code>(0; 1)</code>. We will use the values 0.9, 0.95, and 0.99 to maintain scientific rigor and ease of interpretation, opposite to the [[https://en.wikipedia.org/wiki/Statistical_significance significance level]].
| |
|
| |
| === Assumptions ===
| |
| ;Assumption 1
| |
| : All <code>k</code> centrifuges work continuously and simultaneously for each <code>n</code> cycle with the same <code>τ</code>
| |
| ;Assumption 2
| |
| : There are always enough resources to convert [[uranium-235]] into reactor fuel *
| |
| ;Assumption 3
| |
| : The conversion of [[uranium-235]] into fuel for reactors can be neglected **
| |
| ;Assumption 4 (for long-term play)
| |
| : The game can be played indefinitely (technically assumed for practical use, average playtime suffices)
| |
|
| |
| <nowiki>*</nowiki> For instance, base game [[uranium-238]] has a very high probability (<code>0.993</code>), ensuring a sufficient supply for [[uranium fuel cell]] production.
| |
|
| |
| <nowiki>**</nowiki> For instance, converting base game [[uranium-235]] into 10 [[uranium fuel cell]]s takes <code>12 sec</code>, but the [[reactor]] cycle is <code>200 sec</code> - a negligible time difference, easily managed by building more [[assembler]]s.
| |
|
| |
| === Exact Approach (Short-run)===
| |
| The main question we aim to answer:
| |
|
| |
| <blockquote>
| |
| How many <code>k</code> [[centrifuge]]s are needed during <code>n</code> cycles of [[centrifuge]] production to sustain a [[reactor]] working continuously for <code>T</code> time with probability <code>α</code>?
| |
| </blockquote>
| |
| Assume each [[centrifuge]] in each production cycle is represented by a discrete random variable '''''X<sub>ij</sub>''''', where '''''i''''' is the [[centrifuge]] number and '''''j''''' is the production cycle number. If '''''X<sub>ij</sub>''''' produces [[uranium-235]], its value is <code>X<sub>ij</sub>=1</code>. If not, <code>X<sub>ij</sub>=0</code>. Thus, <code> P(X<sub>ij</sub> = 1) = 0.007</code> and <code> P(X<sub>ij</sub> = 0) = 0.993</code> (This is a [[https://en.wikipedia.org/wiki/Bernoulli_distribution Bernoulli distribution]]).
| |
|
| |
| To find out how long [[centrifuge]]s should produce [[uranium-235]] to sustain a [[reactor]]:
| |
| From one side, the [[reactor]] has <code>T/t</code> working cycles, needing a total of <code>Tc/t</code> [[uranium-235]] to run continuously for time '''''T'''''. Let's denote this value as '''''u''''': <code>u=Tc/t</code>.
| |
| From the other side, the [[centrifuge]]s work continuously for '''''n''''' cycles during time '''''T''''': <code>T = n*τ</code>.
| |
|
| |
| Combining these, our required quantity of '''''u''''' is <code>u=n*τ*c/t</code> for the entire [[reactor]] operation time '''''T'''''.
| |
|
| |
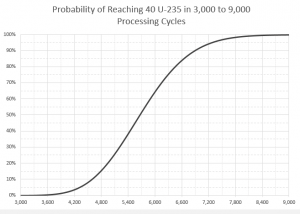
| Consider the simple case where we need '''''n''''' cycles and '''''k''''' [[centrifuge]]s to produce exactly '''''u''''' [[uranium-235]] (technically, we need ceil of '''''u''''', but it won't be practically useful and doesn't detract generality of our calculations). Each '''''X<sub>ij</sub>''''' is a Bernoulli trial, so <code>X<sub>all</sub> = ∑<sub>i</sub><sup>n</sup>∑<sub>j</sub><sup>k</sup>X<sub>ij</sub></code> is the total production, distributed as a [[https://en.wikipedia.org/wiki/Binomial_distribution binomial distribution]] <code>X<sub>all</sub> ~ B(nk, p)</code>. This gives the probability of producing exactly '''''u''''' [[uranium-235]] in '''''n''''' cycles with '''''k''''' [[centrifuge]]s:
| |
| <blockquote>
| |
| <code>P(X<sub>all</sub>=u) = C<sub>nk</sub><sup>u</sup> * p<sup>u</sup> * (1-p)<sup>nk-u</sup></code>
| |
| </blockquote>
| |
| Practically, we are interested in producing at least '''''u''''' [[uranium-235]], corresponding to <code>P(X<sub>all</sub> ≥ u)</code>. This can be calculated as <code>P(X<sub>all</sub> ≥ u) = 1 - P(X<sub>all</sub> < u)</code>, where <code>P(X<sub>all</sub> < u)</code> is the [[https://en.wikipedia.org/wiki/Binomial_distribution#:~=0.059535.-,Cumulative%20distribution%20function,-%5Bedit%5D cumulative distribution function]]:
| |
| <blockquote>
| |
| <code>P(X<sub>all</sub>≥u) ≥ α</code> ⇒ <code>1 - ∑<sub>m</sub><sup>u-1</sup>P(X<sub>all</sub>=m) ≥ α</code> ⇒ {using results from paragraph 1} ⇒ <code>∑<sub>m</sub><sup>n*τ*c/t-1</sup>C<sub>nk</sub><sup>m</sup> * p<sup>m</sup> * (1-p)<sup>nk-m</sup> ≤ 1 - α</code>
| |
| </blockquote>
| |
| So, we now have a formula to determine the number of '''''k''''' [[centrifuge]]s needed to sustain a [[reactor]] with consumption '''''c''''' during '''''n''''' cycles. This formula is general and not always practical for long-term play due to the high values of '''''n''''' and '''''u'''''. It is best suited for short-term or speedrun calculations.
| |
|
| |
| ==== Example Base Game Short-Term ====
| |
| To illustrate, let's determine how many [[centrifuge]]s are needed to sustain 1 [[reactor]] with 0.99 confidence without modules. It's a common mistake to think that 0.007 is the production speed, but it represents the probability of producing [[uranium-235]] per cycle. Suppose we want a reactor to work for 2000 [[centrifuge]] production cycles (about 6.7 hours of reactor operation) with 1 [[centrifuge]]:
| |
|
| |
| {| class="wikitable"
| |
| ! n !! tau !! c !! t !! m !! p !! u !! ceil(u-1) !! alpha !! 1-alpha !! !! k !! C(nk, m) !! P(m) !! ∑<sub>m</sub>P
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 0 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1 || 7,92E-07 || 7,92E-07
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 1 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2000 || 1,12E-05 || 1,20E-05
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 2 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,0E+06 || 7,86E-05 || 9,06E-05
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 3 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1,3E+09 || 0,0004 || 0,0005
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 4 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 6,6E+11 || 0,0013 || 0,0018
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 5 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,7E+14 || 0,0037 || 0,0054
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 6 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 8,8E+16 || 0,0086 || 0,0140
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 7 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,5E+19 || 0,0172 || 0,0312
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 8 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 6,3E+21 || 0,0302 || 0,0302
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 9 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1,4E+24 || 0,0472 || 0,0472
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 10 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 2,8E+26 || 0,0662 || 0,1133
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 11 || 0,007 || 12 || 11 || 0,99 || <span style="color: red">0,01</span> || || 1 || 5,0E+28 || 0,0844 || <span style="color: red">0,1977</span>
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 12 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 8,3E+30 || 0,0986 ||
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 13 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 1 || 1,3E+33 || 0,1063 ||
| |
| |}
| |
|
| |
| As you can see, we need to produce 12 '''''u''''' for 2000 cycles. According to our formula, we need to sum up all the probabilities of producing less than 12 [[uranium-235]] and compare this with our desired confidence level:
| |
|
| |
| <code>∑<sub>m</sub><sup>2000120.1/200-1</sup>C<sub>20001</sub><sup>m</sup> * 0.007<sup>m</sup> * (1-0.007)<sup>20001-m</sup> = 7.92E-07 + 1.12E-05 + 7.86E-05 + 0.0004 + 0.0013 + 0.0037 + 0.0086 + 0.0172 + 0.0302 + 0.0472 + 0.0662 + 0.0844 = 0.1977</code>
| |
|
| |
| We can interpret this value as the "Probability of producing less than the required amount of [[uranium-235]] for 2000 [[centrifuge]] cycles." This probability should be less than <code>1-α = 0.01</code>. However, since it is not, we cannot be sure that 1 [[centrifuge]] will produce enough [[uranium-235]] to sustain [[reactor]] operation during 2000 cycles. Therefore, we need to increase the number of [[centrifuge]]s.
| |
|
| |
| {| class="wikitable"
| |
| ! n !! tau !! c !! t !! m !! p !! u !! ceil(u-1) !! alpha !! 1-alpha !! !! k !! C(nk, m) !! P(x=m) !! sum(P(m<=ceil(u-1)))
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 0 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1 || 6,3E-13 || 6,27E-13
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 1 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 4000 || 1,8E-11 || 1,83E-11
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 2 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 8,0E+06 || 2,5E-10 || 2,67E-10
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 3 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,1E+10 || 2,3E-09 || 2,61E-09
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 4 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,1E+13 || 1,6E-08 || 1,91E-08
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 5 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 8,5E+15 || 9,3E-08 || 1,12E-07
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 6 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 5,7E+18 || 4,4E-07 || 5,48E-07
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 7 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 3,2E+21 || 1,8E-06 || 2,30E-06
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 8 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,6E+24 || 6,2E-06 || 6,17E-06
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 9 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 7,2E+26 || 1,9E-05 || 1,93E-05
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 10 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 2,9E+29 || 0,0001 || 0,0001
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 11 || 0,007 || 12 || 11 || 0,99 || <span style="color: red">0,01</span> || || 2 || 1,0E+32 || 0,0001 || <span style="color: red">0,0002</span>
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 12 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 3,4E+34 || 0,0003 ||
| |
| |-
| |
| | 2000 || 12 || 0,1 || 200 || 13 || 0,007 || 12 || 11 || 0,99 || 0,01 || || 2 || 1,1E+37 || 0,0007 ||
| |
| |}
| |
|
| |
| And now you can see that our condition is fulfilled. Therefore, we can say that without any [[module]]s or [[Kovarex enrichment process]], we can achieve the stability of 1 [[reactor]] during 2000 [[centrifuge]] cycles using at least 2 [[centrifuge]]s! However, does this imply that we need 4 [[centrifuge]]s for 2 [[reactor]]s, 6 [[centrifuge]]s for 3 [[reactor]]s, and so on? I encourage you to think about this question yourself. You may be surprised by the results when applying the approach outlined above.
| |
|
| |
| === Distribution Approximation (Medium-run)===
| |
| If you plan to play for an extended period while your [[reactor]] setup is operating, we can consider <code>n→∞</code>. In this case, since our [[centrifuge]]s' overall production <code>X<sub>all</sub> ~ B(nk, p)</code>, we can use the [[https://en.wikipedia.org/wiki/De_Moivre%E2%80%93Laplace_theorem De Moivre-Laplace theorem]]. In short, it states that if our random variable follows a binomial distribution with a large number of trials, then <code>(X<sub>all</sub>-nkp)/sqrt(nkp(1-p)) ~ N(0, 1)</code>. Thus, to estimate <code>P(X<sub>all</sub> ≥ u)</code>, we simplify it to:
| |
|
| |
| <code>P((X<sub>all</sub>-nkp)/sqrt(nkp(1-p))) ≥ (u-nkp)/sqrt(nkp(1-p)) ≥ α</code> ⇒ <code>{1-P<sub>dist</sub> ≥ α}</code> ⇒ <code>(nkp - u)/sqrt(nkp(1-p)) ≥ ɸ<sup>-1</sup>(1-α)</code>, where ɸ<sup>-1</sup> is the inverse standard normal distribution, found using the [[https://en.wikipedia.org/wiki/Standard_normal_table standard normal table]].
| |
|
| |
| Let's denote <code>ɸ<sup>-1</sup>(α)</code> as λ. For each confidence level α, we can calculate it from the standard normal table:
| |
| <code>λ<sub>0.99</sub>=2.3263</code>, <code>λ<sub>0.95</sub>=1.6449</code>, <code>λ<sub>0.9</sub>=1.2816</code>.
| |
|
| |
| Now we need to solve the equation above for the variable '''''k''''':
| |
|
| |
| <code>(nkp-u)/sqrt(nkp(1-p)) ≥ λ</code> ⇒ <code>(nkp-nτc/t)/sqrt(nkp(1-p)) ≥ λ</code>.
| |
|
| |
| After some basic arithmetic operations and solving the quadratic equation, you can determine the value of '''''k''''':
| |
|
| |
| <blockquote>
| |
| <code>k ≥ [(χ<sub>1</sub> + sqrt(χ<sub>1</sub><sup>2</sup> + 4χ<sub>0</sub>χ<sub>2</sub>))/(2*χ<sub>0</sub>)]<sup>2</sup></code>
| |
| where
| |
| <code>χ<sub>0</sub> = np</code>,
| |
| <code>χ<sub>1</sub> = λ*sqrt(np(1-p))</code>,
| |
| <code>χ<sub>2</sub> = nτc/t</code>,
| |
| <code>λ</code> is the inverse standard normal distribution (popular values: 2.3263; 1.6449; 1.2816 for corresponding α values: 0.99; 0.95; 0.9).
| |
| </blockquote>
| |
|
| |
| This formula can be calculated for very large '''''n'''''. That's why it's best choice for planning average playtime of experienced player.
| |
|
| |
| === Infinite Approximation (Long-run)===
| |
| If we consider the formula for '''''k''''' [[centrifuge]]s above, we can derive an analytical form for <code>n→∞</code> by substituting all '''''χ''''' into the formula and finding the limit:
| |
|
| |
| <blockquote>
| |
| <code>lim<sub>n→∞</sub>(χ<sub>1</sub> + sqrt(χ<sub>1</sub><sup>2</sup> + 4χ<sub>0</sub>χ<sub>2</sub>))/(2*χ<sub>0</sub>)</code> ⇒ {substitute all '''''χ'''''} ⇒ <code>k ≥ τ*c/(p*t)</code>
| |
| </blockquote>
| |
| Thus, to determine the minimal number of [[centrifuge]]s needed to achieve [[reactor]] stability, we use the final formula:
| |
|
| |
| <blockquote>
| |
| <code>k = ⌈τ*c/(p*t)⌉, where ⌈x⌉ is the ceiling function</code>
| |
| </blockquote>
| |
| Notice that this formula does not depend on '''''λ'''''. This is because, as n approaches infinity, the cumulative probability tends to 1. In other words, with an infinite number of cycles, we can be 100% certain that this number of [[centrifuge]]s will sustain our [[reactor]]'s stability indefinitely.
| |
|
| |
| This formula provides the minimal number of [[centrifuge]]s needed to sustain [[reactor]] stability indefinitely. To determine this number, we need only 4 parameters.
| |
| === Conclusion ===
| |
| Through detailed probability calculations and binomial distribution analysis, we have determined the number of [[centrifuge]]s required to sustain a [[reactor]]'s operation. The key findings are:
| |
|
| |
| * Minimum Centrifuges for Reactor Stability: Without any [[module]]s or the [[Kovarex enrichment process]], a minimum of 2 [[centrifuge]]s are needed to ensure the continuous operation of a single [[reactor]] over 2000 cycles with a confidence level of 0.99. However, be careful about using such result for extending it on 2, 3, 4 and more [[reactor]]s, as it will be enough, but not optimal quantity.
| |
|
| |
| * General Formula for Long-Term Play: For an infinite number of cycles, the formula <code>k = ⌈τ * c / (p * t)⌉</code> provides the minimal number of [[centrifuge]]s required to sustain [[reactor]] stability indefinitely. This formula is derived from the behavior of the binomial distribution as the number of cycles approaches infinity. The derived formula for the infinite approximation does not depend on the confidence interval parameter '''''λ''''' and cycles '''''n''''', making it robust and straightforward to apply for long-term game planning.
| |
|
| |
| * As these results are based on using abstract recipe cycle of [[centrifuge]]s, it doesn't depend on in-game [[tick]]s implementation and real time estimation.
| |
|
| |
| * Probability estimation for short-term of [[centrifuge]]s produce desired amount of [[uranium-235]].
| |
|
| |
| * We derived 2 important formulas:
| |
|
| |
| ;Medium-term
| |
| : <code>k = ⌈[(χ<sub>1</sub> + sqrt(χ<sub>1</sub><sup>2</sup> + 4χ<sub>0</sub>χ<sub>2</sub>))/(2*χ<sub>0</sub>)]<sup>2</sup>⌉</code>
| |
| where
| |
| <code>χ<sub>0</sub> = np</code>,
| |
| <code>χ<sub>1</sub> = λ*sqrt(np(1-p))</code>,
| |
| <code>χ<sub>2</sub> = nτc/t</code>,
| |
| <code>λ</code> is the inverse standard normal distribution
| |
| ;Long-term
| |
| : <code>k = ⌈τ*c/(p*t)⌉</code>
| |
|
| |
| * Rule of thumb: If you need to quickly estimate how many [[centrifuge]]s are required to initiate and maintain the stability of [[reactor]]s in the medium term (over the next few hours), just build an additional 1/3 of the long-term value. From Example 2, you can use the golden ratio and build 1.15 [[centrifuge]]s per [[reactor]] to ensure stability.
| |
|
| |
| === Usage examples ===
| |
| ====Example 1====
| |
| [[File:Comparing calculations example1.png|300px|thumb|right|2 methods convergence comparison (example 1)]]
| |
|
| |
| Let's find out how many [[centrifuge]]s do you need for playing long-run playtime and average playtime for 20 [[reactor]]s without any [[module]]s and [[kovarex enrichment process]].
| |
|
| |
| First of all, notice that we can pretend that 20 [[reactor]]s are just one big reactor and the only parameter that will be influenced is '''''c'''''. As we have 20 times more reactors, that means that our default consumption will be 20 times more, then we have <code>c = 20*0.1 = 2</code>. So now we can use 2 methods for long-run and medium-run estimations:
| |
|
| |
| Long-run doesn't depend on '''''n''''' that's why we can easily calculate it: <code>k=⌈τ*c/(p*t)⌉=18</code>.
| |
|
| |
| Medium-run has explicit formula, but need to iterate over '''''n'''''. I've built a graph to explicitly show, that after many [[centrifuge]]s cycles, medium-run amount of '''''k''''' tends to Long-run amount. If we take 1000 cycles and 0.99 confident level, then k = 22. On the other side, 1000 cycles is equal to 3.33 hours. This is the main reason why you need understand importance of both estimations. As after setting [[centrifuge]] configuration by long-term value, you won't be stable after 3.3 hours and there can be shortages in [[uranium-235]] production.
| |
|
| |
| ====Example 2 (Golden ratio)====
| |
| Assume that the [[reactor]]'s consumption depends only on the total number of [[reactor]]s and consider a long-term play scenario. In the base game, we know that each [[reactor]] consumes 1/10 of a unit of [[uranium-235]] per [[reactor]] cycle.
| |
|
| |
| This leads us to <code>c = 0.1 * R</code>, where <code>R</code> is the number of [[reactor]]s. Using the long-term formula, we can derive the optimal [[centrifuge]] to [[reactor]] ratio:
| |
|
| |
| <code>k / R = τ / (10 * p * t)</code>
| |
|
| |
| If you are playing without [[module]]s, the value is: <code>12 / (10 * 0.007 * 200) = 0.8571</code>. So, if you have 4 [[reactor]]s, you will need at least 4 [[centrifuge]]s for long-term stability.
| |
| == History == | | == History == |
| {{History|0.15.0| | | {{History|0.15.0| |