ウラン濃縮処理

ウラン濃縮処理

Edit

レシピ
12 + 10 → 0.007 + 0.993
トータルコスト
12 + 10
Prototype type	recipe
Internal name	uranium-processing
必要なテクノロジー
製作可能設備

ウラン濃縮処理はウラン鉱石の唯一の使い道であり、プレイヤーにとって、最初のウラン-235とウラン-238をもたらすものである。この処理は、99.3%の確率でウラン-238を１個、0.7%の確率でウラン-235を１個生産する。

Kovarex濃縮プロセスの開始

ゲーム中の他の製造過程と違い、ウラン濃縮処理はU-235とU-238を、決定論的に保証された量ではなく、確率的に生産する。加えて、Kovarex濃縮プロセスは、１台の遠心分離機で開始するために、希少なウラン-235同位体を40個も備蓄する必要がある。そのため、Kovarex濃縮プロセスでのウラン採掘と加工を計画するときは、ゲームの他の部分とは異なる考慮が必要になる。

期待値

遠心分離機でウラン濃縮処理を行って、p = 0.007でU-235が作られるので、１個得るまでに必要な処理サイクル数の期待値は、E(1,p) = 1 ÷ p = ~143 である。40個得るまでに必要なサイクル数の期待値は、E(40,p) = 40 × E(1,p) = ~5,714 cycles となる。このように沢山の処理を行うには、ウラン鉱石を57,140個採掘する必要がある。簡単な仕事ではない。

しかし、確率の性質上、これだけのサイクルで40個を保証することはできない。実のところ、5,714サイクルで少なくとも40ユニットのU-235が生成される確率は、数学的に約52％に過ぎない。

信頼水準

ウラン濃縮処理のサイクル数によってU-235が40個手に入る確率（クリックして拡大）

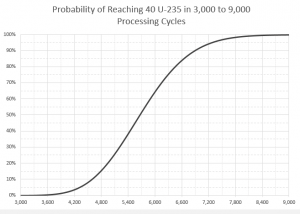
さらに数学を用いれば、信頼水準（設定された目標を達成する確率）を考慮して、少なくとも40個のU-235を（p = 0.007とすると）得るために実行しなければならないウラン処理サイクルの数を計算することができる。

前節で述べたように、5,714サイクル（得られたU-235の期待値が40個である場合）に対応する信頼水準は約52％である（言い換えれば、このサイクル数では、2回に1回弱の割合でU-235が40個に達しないことが期待できる）。

プレイヤーが興味を持ちそうな信頼水準の例をいくつか下の表に示す。その他の具体的な値については右のグラフを参照してください。

信頼水準	失敗	必要なサイクル数
10%	10回中9回	4,595
50%	2回中1回	5,667
90%	10回中1回	6,894
95%	20回中1回	7,272
99%	100回中1回	8,015

精密な数学的分析

Kovarex濃縮プロセスを使わずに、原子炉を安定的に維持するために必要な遠心分離機の数を正確に決めるには、確率論を使う必要がある。この分析は、必要な量のウラン-235が得られる確率と、必要な遠心分離機の数を見積もるのに役立つ。

これらの計算の主な目的は、技術の進歩、ゲームバージョンの更新、またはゲーム内の開発や修正にもかかわらず、簡単に適用でき、持続ｗｗ的に予測可能な式を導き出すことである。

変数

以降の計算に必要な変数を導入しよう。

• T - 原子炉が稼働する総時間 (秒単位*)
• t - 原子炉のサイクル時間 (秒単位*)
• c - 原子炉1サイクルあたりのウラン-235の消費
• k - 遠心分離機の数 (計算する目標の値)
• p - 遠心分離機１サイクルあたりのウラン-235生産確率
• n - 遠心分離機サイクルの総回数
• τ - 遠心分離機が１レシピ生産するためのサイクル時間
• α - 原子炉が時間T安定稼働するために必要なウラン-235が手に入る確率の希望値**

* 秒またはゲーム内ティックで計測される。これは一般的な推論には影響しない。

** [信頼水準]として知られる。確率論の性質上、この値は0から1の間になる。科学的な厳密さと解釈のしやすさを維持するため、[有意水準]とは逆の0.9、0.95、0.99を使用する。

前提条件

前提条件 1

k個の遠心分離機はすべて継続的かつ同時並行で、各nサイクルを、同じτ時間稼働する。

前提条件 2

ウラン-235を燃料棒に変換するための資源は常に十分にある。*

前提条件 3

ウラン-235から燃料棒への変換は無視できる。**

前提条件 4 (長期間のプレイ向け)

ゲームは無期限にプレイできる（技術的には、実用上は平均的なプレイ時間で十分である）

* 例えば、基本ゲームのウラン-238は非常に高い確率(0.993)で入手できるため、燃料棒を製造するのに十分な供給があると思われる。

** 例えば、基本ゲームでウラン-235から燃料棒10個を製造するのに12 秒かかるが、原子炉のサイクルは200 秒である。無視できるほど異なる時間であり、沢山の組立機を建てることで容易にやりくりできる。

厳密なアプローチ (短期)

答えを導こうとしている主な問いは以下のとおりである。

遠心分離機がn回生産する間に、原子炉をT秒間連続稼働するのに必要な量を、αの確率で入手するために、遠心分離機が必要な数kはいくつか。

各遠心分離機の生産サイクルを離散的確率変数X_ijとする。ここで、iは遠心分離機の番号、jは生産サイクルの番号とする。 X_ijでウラン-235が得られるならば、その値はXij=1とする。そうでない場合は、Xij=0とする。つまり、 P(Xij = 1) = 0.007であり、 P(Xij = 0) = 0.993である。（これは、[ベルヌーイ分布]である）

遠心分離機が原子炉の維持に必要なウラン-235を生産するのにどのくらいの期間稼働するかを求めるには、以下のようにする。 ある側面では、原子炉はT/tサイクル稼働することになるので、T秒間の運転にはウラン-235は合計でTc/t個必要となる。この値を、uで表そう。u=Tc/tである。 別の側面では、遠心分離機はT秒間にnサイクル稼働することになるので、T = n*τである。

これらを組み合わせると、必要とするuの値は、原子炉が稼働する時間Tに対しては、u=n*τ*c/tで表せる。

正確にu個のウラン-235（技術的には、uを切り上げる必要があるが、実用的でないし、計算の汎用性を損なうものでもない）を生産するには、n回のサイクルとk個の遠心分離機が必要という、単純な場合を考えてみる。それぞれのX_ijはベルヌーイ試行であるため、Xall = ∑in∑jkXijが総生産量となり、[二項分布] Xall ~ B(nk, p)にしたがう。これによって、正確にu個のウラン-235を、n回のサイクルとk個の遠心分離機で生産する確率が求められる。

P(Xall=u) = Cnku * pu * (1-p)nk-u

実用上は、最低でも u個のウラン-235を生産することに関心があり、これは P(Xall ≥ u) といえる。P(Xall ≥ u) = 1 - P(Xall < u) で計算でき、P(Xall < u) は [累積分布関数] である。

P(Xall≥u) ≥ α ⇒ 1 - ∑mu-1P(Xall=m) ≥ α ⇒ {段落1の結果より} ⇒ ∑mn*τ*c/t-1Cnkm * pm * (1-p)nk-m ≤ 1 - α

これで、c個消費する原子炉を維持するために必要な遠心分離機の数kと、サイクル数nを決定する数式が手に入った。この数式は一般的であるが、常に実用的なわけではない。特に長時間のプレイになると、n と u の値が大きくなってしまうためである。短期間のプレイやスピードランのための計算に最も適している。

基本ゲームでの短期間の例

モジュールなしの原子炉1基を信頼水準0.99で稼働させるために、何台の遠心分離機が必要になるか求めてみよう。 0.007を生産速度だと考えるのはよくある間違いである。これは、サイクルごとにウラン-235が生産される確率を表している。 遠心分離機１台で、原子炉を遠心分離機の生産サイクル2000回分稼働させる（つまり原子炉を約6.7時間稼働させる）と仮定すると、

n	tau	c	t	m	p	u	ceil(u-1)	alpha	1-alpha		k	C(nk. m)	P(m)	∑mP
2000	12	0.1	200	0	0.007	12	11	0.99	0.01		1	1	7.92E-07	7.92E-07
2000	12	0.1	200	1	0.007	12	11	0.99	0.01		1	2000	1.12E-05	1.20E-05
2000	12	0.1	200	2	0.007	12	11	0.99	0.01		1	2.0E+06	7.86E-05	9.06E-05
2000	12	0.1	200	3	0.007	12	11	0.99	0.01		1	1.3E+09	0.0004	0.0005
2000	12	0.1	200	4	0.007	12	11	0.99	0.01		1	6.6E+11	0.0013	0.0018
2000	12	0.1	200	5	0.007	12	11	0.99	0.01		1	2.7E+14	0.0037	0.0054
2000	12	0.1	200	6	0.007	12	11	0.99	0.01		1	8.8E+16	0.0086	0.0140
2000	12	0.1	200	7	0.007	12	11	0.99	0.01		1	2.5E+19	0.0172	0.0312
2000	12	0.1	200	8	0.007	12	11	0.99	0.01		1	6.3E+21	0.0302	0.0302
2000	12	0.1	200	9	0.007	12	11	0.99	0.01		1	1.4E+24	0.0472	0.0472
2000	12	0.1	200	10	0.007	12	11	0.99	0.01		1	2.8E+26	0.0662	0.1133
2000	12	0.1	200	11	0.007	12	11	0.99	0.01		1	5.0E+28	0.0844	0.1977
2000	12	0.1	200	12	0.007	12	11	0.99	0.01		1	8.3E+30	0.0986
2000	12	0.1	200	13	0.007	12	11	0.99	0.01		1	1.3E+33	0.1063

見ての通り、2000サイクルのうちに、u=12個のウランを生産する必要がある。数式によれば、ウラン-235が12個より少なくなる場合の確率をすべて合計したものを、希望する信頼水準と比較することになる。

∑m2000120.1/200-1C20001m * 0.007m * (1-0.007)20001-m = 7.92E-07 + 1.12E-05 + 7.86E-05 + 0.0004 + 0.0013 + 0.0037 + 0.0086 + 0.0172 + 0.0302 + 0.0472 + 0.0662 + 0.0844 = 0.1977

この値は、「遠心分離機2000サイクルで必要な量のウラン-235が生産できる確率が足りない」と解釈できる。この確率は、1-α = 0.01未満でなければならない。しかし、そうなってはいないので、1台の遠心分離機が2000サイクルの間で、原子炉の運転を維持するのに十分な量のウラン-235を生産するとは言えない。故に、遠心分離機の台数を増やす必要がある。

n	tau	c	t	m	p	u	ceil(u-1)	alpha	1-alpha		k	C(nk. m)	P(x=m)	sum(P(m<=ceil(u-1)))
2000	12	0.1	200	0	0.007	12	11	0.99	0.01		2	1	6.3E-13	6.27E-13
2000	12	0.1	200	1	0.007	12	11	0.99	0.01		2	4000	1.8E-11	1.83E-11
2000	12	0.1	200	2	0.007	12	11	0.99	0.01		2	8.0E+06	2.5E-10	2.67E-10
2000	12	0.1	200	3	0.007	12	11	0.99	0.01		2	1.1E+10	2.3E-09	2.61E-09
2000	12	0.1	200	4	0.007	12	11	0.99	0.01		2	1.1E+13	1.6E-08	1.91E-08
2000	12	0.1	200	5	0.007	12	11	0.99	0.01		2	8.5E+15	9.3E-08	1.12E-07
2000	12	0.1	200	6	0.007	12	11	0.99	0.01		2	5.7E+18	4.4E-07	5.48E-07
2000	12	0.1	200	7	0.007	12	11	0.99	0.01		2	3.2E+21	1.8E-06	2.30E-06
2000	12	0.1	200	8	0.007	12	11	0.99	0.01		2	1.6E+24	6.2E-06	6.17E-06
2000	12	0.1	200	9	0.007	12	11	0.99	0.01		2	7.2E+26	1.9E-05	1.93E-05
2000	12	0.1	200	10	0.007	12	11	0.99	0.01		2	2.9E+29	0.0001	0.0001
2000	12	0.1	200	11	0.007	12	11	0.99	0.01		2	1.0E+32	0.0001	0.0002
2000	12	0.1	200	12	0.007	12	11	0.99	0.01		2	3.4E+34	0.0003
2000	12	0.1	200	13	0.007	12	11	0.99	0.01		2	1.1E+37	0.0007

条件が満たされていることがご覧いただけるだろう。故に、モジュールやkovarex濃縮プロセスなしに、原子炉1基を遠心分離機2000サイクルの間安定的に稼働させるには、少なくとも遠心分離機が2台必要と言える。しかし、これは2台の原子炉のために4台の遠心分離機が必要、3台の原子炉のために6台の遠心分離機が必要、ということを意味しているのだろうか？この質問について自分で考えてみることをお勧めする。上記のアプローチを適用すると、その結果に驚くかもしれない。

分布の近似（中期）

原子炉のセットアップを稼働させたまま、長期間プレーする予定がある場合は、n→∞（nを無限に近づける）を検討することができる。この場合、遠心分離機の生産総量はXall ~ B(nk, p)となるので、[ド・モアブル=ラプラスの極限定理]が使える。要するに、乱数が二項分布に従うとき、試行回数の多い場合は、次のようになる。(Xall-nkp)/sqrt(nkp(1-p)) ~ N(0, 1) 従って、P(Xall ≥ u) を推定するには、単に以下のようにすれば良い。 P((Xall-nkp)/sqrt(nkp(1-p))) ≥ (u-nkp)/sqrt(nkp(1-p)) ≥ α ⇒ {1-Pdist ≥ α} ⇒ (nkp - u)/sqrt(nkp(1-p)) ≥ ɸ-1(1-α) ここで、 ɸ^-1 は標準正規分布の逆数である。[正規分布表]を使う。

ɸ-1(α) を λ とする。各信頼水準 α ごとに、正規分布表から、以下のように計算できる。 λ0.99=2.3263, λ0.95=1.6449, λ0.9=1.2816.

今度は、上の方程式を変数kについて解く必要がある。

(nkp-u)/sqrt(nkp(1-p)) ≥ λ ⇒ (nkp-nτc/t)/sqrt(nkp(1-p)) ≥ λ.

いくつかの基本的な算術演算と二次方程式を解くと、k の値を求めることができる。

k ≥ [(χ1 + sqrt(χ12 + 4χ0χ2))/(2*χ0)]2 ここで、 χ0 = np, χ1 = λ*sqrt(np(1-p)), χ2 = nτc/t, λ は標準正規分布の逆数である (よく知られた値は、α の値 0.99; 0.95; 0.9 について、2.3263; 1.6449; 1.2816 である).

この数式は、非常に大きいnでも計算できる。だからこそ、経験豊富なプレーヤーの平均的なプレー時間を計画するのに最適な選択なのだ。

無限の近似 (長期)

上の方のk個の遠心分離機の公式について考えるならば、公式にすべてのχを代入して、n→∞ の解析系を導き、極限を見つけることができる。

limn→∞(χ1 + sqrt(χ12 + 4χ0χ2))/(2*χ0) ⇒ {すべての χ を代入する} ⇒ k ≥ τ*c/(p*t)

結果として、原子炉を安定稼働させるために必要な遠心分離機の最小数を求めるには、以下の公式を使えば良い。

k = ⌈τ*c/(p*t)⌉, ここで ⌈x⌉ は切り上げることを表す。

この公式にλが含まれていないことに注意しよう。これは、nが無限に近づくと、累積確率は１に近づくからである。言い換えれば、この数の遠心分離機でサイクル数を無限にすれば、原子炉の安定稼働は100%達成できるということである。

この公式が、原子炉をいつまでも安定稼働させるために必要な遠心分離機の最小数を与えてくれる。この数字を決定するためには、４つのパラメータしか必要としない。

結論

詳細な確率の計算や二項分布の解析を通じて、原子炉の稼働に必要な遠心分離機の数を決定することができた。 重要な発見は以下の通りである。

• 原子炉の安定稼働のための遠心分離機の最小数：モジュールやKovarex濃縮プロセスなしで、原子炉１基を2000サイクル以上、信頼水準 0.99 で安定稼働させるには、最低でも２個の遠心分離機が必要になる。しかし、この結果を2, 3, 4個以上の原子炉に拡張する場合は注意すること。それは十分かもしれないが、最適な量ではない。

• 長期間の場合の一般公式：サイクル数を無限にする場合、k = ⌈τ * c / (p * t)⌉ という公式が、原子炉をいつまでも稼働させるのに必要な遠心分離機の最小数を与えてくれる。この公式は、二項分布の試行回数を無限に近づけることで導かれる。無限に近似して導かれた公式は、信頼水準のパラメータλやサイクル数nを含んでおらず、長期間のプレイに適用できる堅牢さと明快さを備えている。

• これらの結果は、遠心分離機のレシピサイクルを抽象化して使用しており、ゲーム内のティックや実時間の見積もりには依存しない。

• 遠心分離機が希望する量のウラン-235を製造するのに要する時間の確率推定。

• We derived 2 important formulas:
• ２つの重要な公式を導いた。

中期

k = ⌈[(χ1 + sqrt(χ12 + 4χ0χ2))/(2*χ0)]2⌉

ここで、 χ0 = np, χ1 = λ*sqrt(np(1-p)), χ2 = nτc/t, λ は標準正規分布の逆数とする。

長期

k = ⌈τ*c/(p*t)⌉

• 大まかなやり方：原子炉の安定運用に必要な遠心分離機の数について、中期（これからの数時間以上）の見積もりを素早く計算する必要がある場合は、長期の値を３割増にして建設すればよい。例２から、黄金比を使う事で、原子炉１基につき、遠心分離機1.15個という数字が使える。

使い方の例

例1

２つの方法が収束する様子（例１）

長期間のプレイと平均的なプレイ時間とで、20基の原子炉を、モジュールやkovarex濃縮プロセスを使わずに動作させるには、いくつのcentrifuge/ja遠心分離機が必要になるか求めてみよう。

まず初めに、原子炉20基は、一つの巨大な原子炉とみなせることに注意。そして、変数 c の影響しか受けない。 原子炉が20倍多いということは、デフォルトの消費量が20倍になるということであり、c = 20*0.1 = 2となる。これで、長期と中期の推定に2つの方法を使うことができる：

長期の場合は、n によらないので、簡単に計算できる。k=⌈τ*c/(p*t)⌉=18 となる。

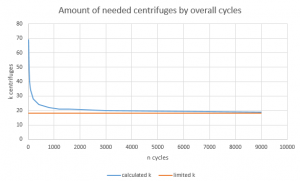
中期の場合には明確な式があるが、n回繰り返し計算する必要がある。遠心分離機のサイクルを何回も繰り返した後、中期のkの値が長期の値に近づく傾向があることを明示的に示すためにグラフを作成した。仮に1000サイクルと0.99の信頼水準をとると、k = 22となる。一方、1000サイクルは3.33時間に相当する。これが、両方の見積もりの重要性を理解する必要がある主な理由である。長期的な値で遠心分離機の構成を設定すると、3.3時間後に安定しなくなり、ウラン-235の生産が不足する可能性があるからである。

例2 (黄金比)

原子炉の消費量は原子炉の総数にのみ依存すると仮定し、長期的なプレイシナリオを考える。基本ゲームでは、各原子炉が原子炉1サイクルあたり1/10単位のウラン235を消費することが分かっている。

結果として、c = 0.1 * R となる。ここで、R は原子炉の総数である。長期の式を使うと、最適な遠心分離機 と 原子炉 の比率を求められる。

k / R = τ / (10 * p * t)

モジュールを使わないのであれば、この値は 12 / (10 * 0.007 * 200) = 0.8571 となる。もし、原子炉が4基なら、少なくとも遠心分離機4台が長期的な安定稼働に必要ということになる。

関連項目

• Kovarex濃縮プロセス