Tutorial:Angewandte Leistungsmathematik

In diesem Tutorial werden wir die Frage beantworten: Wie viel Kohle wird für den Betrieb einer Fabrik benötigt?

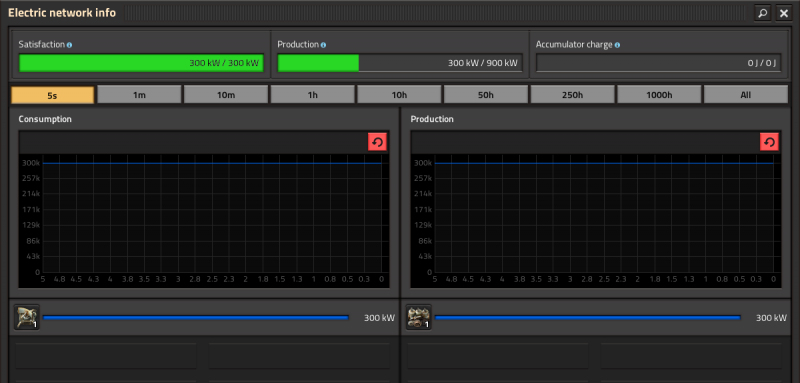
Zunächst einmal müssen wir wissen: Wie viel Strom verbraucht unsere Fabrik? Das ist ganz einfach - man kann in den Stromnetz-Informationen nachsehen, indem man auf einen Strommast klickt.

Hier sehen wir ein Radar, das 300 kW verbraucht. Factorio wendet hier echte Wissenschaft an. Ein Watt (W) ist das Maß für die Energieübertragung. Ein Kilowatt (kW) ist 1000 W, ein Megawatt (MW) ist 1000 kW, und wenn man das Glück hat, eine Fabrik zu bauen, die groß genug ist, ist ein Gigawatt (GW) 1000 MW.

Damit ist die Frage beantwortet, wie viel Strom unsere Fabrik verbraucht. Um unsere Fabrik auf Hochtouren laufen zu lassen, brauchen wir 300 kW. Um den Vergleich zu vereinfachen, rechnen wir das in 0,3 MW um.

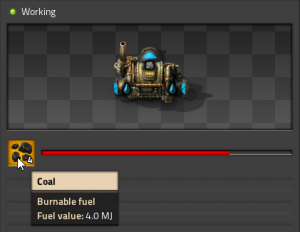
Nächste Frage! Wie viel Energie ist in der Kohle gespeichert? Auch das ist einfach, denn sie sagt es uns, wenn wir die Maus darüber halten: 4 MJ.

Ein Joule ist wieder ein Standardmaß für gespeicherte Energie. Wie bei den Watt ist ein Kilojoule (kJ) gleich 1000 J, und so weiter. Es besteht ein festes Verhältnis zwischen Joule und Watt. 1 Joule kann 1 Sekunde lang 1 Watt Leistung liefern. Als Formel:

   J = W × s

Um unsere Fabrik mit 0,3 MW zu betreiben, müssen wir also jede Sekunde 0,3 MJ verbrauchen.

Quiz

Wie lange kann ein Stück Kohle (4 MJ) unser einzelnes Radargerät (0,3 MW) betreiben?

Erweitern, um die Antwort anzuzeigen

   4 MJ = 0,3 MW × s
      s = 4 MJ ÷ 0,3 MW
      s = 13,33

Etwas mehr als 13 Sekunden.

Wie groß ist die größte Fabrik (in Watt), die ein einzelnes Stück Kohle 5 Sekunden lang betreiben kann?

Erweitern, um die Antwort anzuzeigen

   4 MJ = MW × 5
     MW = 4 MJ ÷ 5
     MW = 0,8

0,8 Megawatt.

BONUS! Eine Tonne Kohle aus der realen Welt enthält etwa 21 GJ. Wie viel wiegt ein Stück Factorio-Kohle?

Erweitern, um die Antwort anzuzeigen

Die Energieverhältnisse dürften mit den Gewichtsverhältnissen übereinstimmen, also:

   4 MJ / 21000 MJ = Gewicht ÷ 1000 KG
            Gewicht = (4 MJ ÷ 21000 MJ) × 1000 KG
            Gewicht = 0,19 KG

Etwa 190 g! Das erklärt immer noch nicht, wie unsere Figur so viel davon tragen kann...

Jetzt haben wir alles, was wir brauchen, um unsere Ausgangsfrage zu beantworten: Wie viel Kohle brauchen wir für den Betrieb unserer Fabrik? Nun, die Frage muss eigentlich ein bisschen präziser sein: Wie viel Kohle brauchen wir pro Sekunde für den Betrieb unserer Fabrik?

Übrigens: Warum lief das Radar für 20s und nicht für 13,5s (50% von 27s)?

Weil es sich nicht immer komplett ein- oder ausschaltet. Wie man in der Grafik sehen kann, steigt der Energieverbrauch an fällt dann wieder ab. Wenn man die Fläche unter der Kurve messen würde, ergäbe das die erwarteten 4 MJ.

Quiz

Wie viel Kohle pro Sekunde wird für den Betrieb einer 20-MW-Fabrik benötigt?

Erweitern, um die Antwort anzuzeigen

Da J = W × s, verbraucht eine 20-MW-Fabrik 20 MJ/s. Da Kohle 4 MJ enthält, benötigen wir 5 Kohle pro Sekunde (5 × 4 MJ = 20 MJ).

BONUS! Wie viele Erzförderer sind erforderlich, um diese Menge Kohle zu produzieren?

Erweitern, um die Antwort anzuzeigen

Aus der verlinkten Seite geht hervor, dass ein elektrischer Erzförderer 0,5/s produziert, also brauchen wir 10 elektrische Erzförderer (10 × 0,5 = 5).

ZWEITER BONUS! Der durchschnittliche deutsche 3-Personen-Haushalt verbrauchte 2019 1,476 GJ im Monat (üblicherweise ausgedrückt als 410 Kilowattstunden). Wie viel Factorio-Kohle wäre nötig, um einen dieser Haushalte in diesem Zeitraum mit Strom zu versorgen, und wie viele Haushalte könnte eine Dampfmaschine (900 kW) versorgen, vorausgesetzt, der Strom wird konstant verbraucht? (Gehen wir von 30 Tagen im Monat aus.)

Erweitern, um die Antwort anzuzeigen

   1,476 GJ = 1476 MJ
   1476 MJ ÷ 4 MJ = 369

   1476 MJ ÷ 30 days ÷ 24 hours ÷ 60 minutes ÷ 60 seconds = 569,4 W
   900.000 W ÷ 569,4 W = 1580,5

369 Kohlestücke pro Haushalt, und eine einzelne Dampfmaschine könnte genau 1580 Haushalte versorgen.