Tutorial:Solar power math: Difference between revisions
Use gallery instead of tabber |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Languages}} | |||
In this tutorial we will properly quantify the amount of [[solar panel]]s and [[accumulator]]s needed and the proper ratio that is needed between the two buildings. | In this tutorial we will properly quantify the amount of [[solar panel]]s and [[accumulator]]s needed and the proper ratio that is needed between the two buildings. | ||
| Line 100: | Line 101: | ||
</div> | </div> | ||
</div> | </div> | ||
Knowing how much power a solar panel provides on average we can construct a fitting load to test how much max accumulator charge <math>\hat{A}</math> is needed. | Knowing how much power a solar panel provides on average we can construct a fitting load to test how much max accumulator charge <math>\hat{A}</math> is needed. | ||
| Line 110: | Line 109: | ||
* 1/0 regular inserters (400 W per unit). | * 1/0 regular inserters (400 W per unit). | ||
To that we add a generous 100 accumulators and observe the energy in the system. | To that we add a generous 100 accumulators and observe the energy in the system. | ||
< | <gallery mode="slideshow"> | ||
41.9 kW grid | File:Solar_panel_with_load_41point9kW.png|41.9 kW grid | ||
File:Solar_panel_with_load_42kW.png|42 kW grid | |||
42 kW grid | File:Solar_panel_with_load_42kW_zoom.png|42 kW grid (zoomed in) | ||
</gallery> | |||
42 kW grid (zoomed in) | |||
</ | |||
Experimental values for the 41.9 kW grid show the first peak has a height of about 4.24 MJ, with each consecutive peak growing higher as the true output of a solar panel is indeed more than 41.9 kW.<br> | Experimental values for the 41.9 kW grid show the first peak has a height of about 4.24 MJ, with each consecutive peak growing higher as the true output of a solar panel is indeed more than 41.9 kW.<br> | ||
Experimental values for the 42 kW grid show each peak reaching about 4.24 MJ, but falling short for 5 seconds. | Experimental values for the 42 kW grid show each peak reaching about 4.24 MJ, but falling short for 5 seconds if it has to start from no charge at all. This may be due to the fact that machines start to behave differently when power is low. However, if we start the experiment with some slight pre-existing charge, the system will be stable. | ||
== Accumulators per solar panel == | |||
4.24 MJ is enough to fill 0.848 accumulators as they can hold a charge of 5 MJ each. Conservatively we can therefore set 0.85 accumulators per solar panel, or a ratio of 20 solar panels to 17 accumulators. A less conservative approach is to use 0.84 accumulators per solar panel, or a ratio of 25 solar panels to 21 accumulators. | 4.24 MJ is enough to fill 0.848 accumulators as they can hold a charge of 5 MJ each. Conservatively we can therefore set 0.85 accumulators per solar panel, or a ratio of 20 solar panels to 17 accumulators. A less conservative approach is to use 0.84 accumulators per solar panel, or a ratio of 25 solar panels to 21 accumulators. | ||
| Line 286: | Line 285: | ||
The most commonly recommended ratio is 21/25 or 0.84, let's see how it fairs against 17/20 or 0.84, and then check out ratios for 0.8467 and 0.8469. And for fairness, these tests start off with fully charged accumulators before a load is applied. | The most commonly recommended ratio is 21/25 or 0.84, let's see how it fairs against 17/20 or 0.84, and then check out ratios for 0.8467 and 0.8469. And for fairness, these tests start off with fully charged accumulators before a load is applied. | ||
< | <gallery mode="slideshow"> | ||
84/100 (21/25 or 0.84) | File:Solar_panel_21to25.png|84/100 (21/25 or 0.84)<br>fell 0 kJ accumulator charge for 18 seconds | ||
File:Solar_panel_17to20.png|85/100 (17/20 or 0.85)<br>lowest recorded accumulator charge: 959 kJ (11.282 kJ per accumulator) | |||
fell 0 kJ accumulator charge for 18 seconds | File:Solar_panel_83to98.png|83/98 (or 0.8469)<br>lowest recorded accumulator charge: 107 kJ (1.289 kJ per accumulator) | ||
File:Solar_panel_116to137.png|116/137 (or 0.8467)<br>fell 0 kJ accumulator charge for half a second | |||
85/100 (17/20 or 0.85) | </gallery> | ||
lowest recorded accumulator charge: 959 kJ (11.282 kJ per accumulator) | |||
83/98 (or 0.8469) | |||
lowest recorded accumulator charge: 107 kJ (1.289 kJ per accumulator) | |||
116/137 (or 0.8467) | |||
fell 0 kJ accumulator charge for half a second | |||
</ | |||
The tests support the analytic solution. The ratio for 0.8467 barely falls short of being able to sustain 42 kW of power, while 0.8469 almost fully discharges to 0.025%. | The tests support the analytic solution. The ratio for 0.8467 barely falls short of being able to sustain 42 kW of power, while 0.8469 almost fully discharges to 0.025%. | ||
Latest revision as of 16:12, 5 March 2025
In this tutorial we will properly quantify the amount of solar panels and accumulators needed and the proper ratio that is needed between the two buildings.
Equation symbols and units
The game uses SI units and reflects how they are used in the real world. Energy and power are often used interchangeably, but power is the first time derivative of energy, i.e. how much energy is used or produced per second. Power can be used to get machines moving, as they perform work . A type of work can be lifting some mass against gravitational acceleration for a set distance. Usually there is always a loss of usable energy due to thermal energy being released, but Factorio does not take such losses into consideration. Lastly there is the charge in accumulators. Charge traditionally has the unit Coulomb and the energy in a capacitor depends on the charge and the voltage across it, but as Factorio also doesn't consider equipment using different voltages, a the charge of a factorio-accumulator can be defined to use this combined value.
Therefore the important equation symbols for energy are as follows:
- ... energy, in Joule, also often written in kilowatt-hours, where .
- ... performed work, in or Newton-meter which is equal to Joule
- ... accumulator charge, in Joule
And the important equation symbols for power are as follows, with dot-notation for the time derivative:
- ... supplied power, in Watt, or Joule per second.
- ... ongoing mechanical work, in Watt
- ... change in accumulator charge, in Watt
Energy can't be generated or destroyed, only converted into a different form. This means that the balance of energy must be upheld, and therefore its rate of change must be zero. If we subtract from the supplied power both the ongoing mechanical work and the rate at which accumulators are charging (therefore taking energy from the grid), the result will be zero. As such we can write
.
The player will not have to worry about overproduction, as any power generating equipment will cap its output automatically. Only too little production will no longer provide machines with the amount of power that they desire, causing them to throttle their own power demand and working slower. Therefore in almost all cases these rates will change over time, where solar panels produce energy dependant on the time of day, while machines equally draw more or less power depending on how much they are used. For example, inserters only draw their power when they swing their arms, while only using a tiny fraction of it on standby. As such we introduce notation for various statistically relevant values.
- Average value over an interval is annotated with a bar above:
- Peak value with an upward facing chevron:
Average output of 1 solar panel
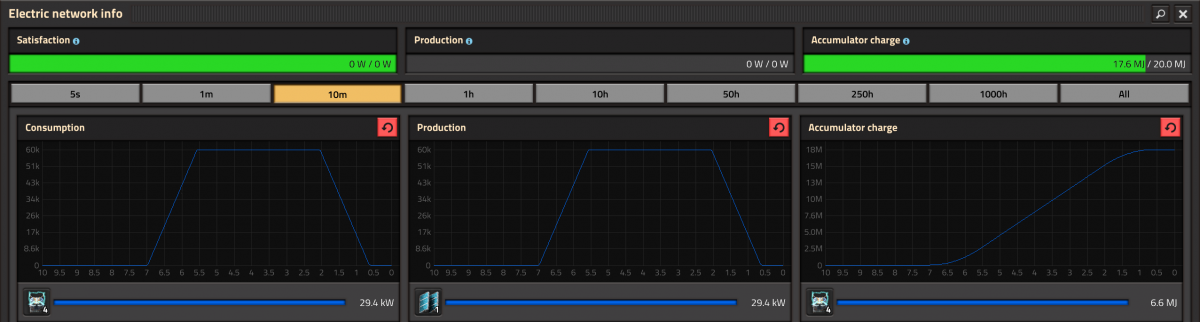
While only the peak output of a solar panel can be easily be told at , its exact power output over the day changes with available daylight. Thankfully, if we install some accumulators, they can do the integration for us.
In an experiment with one solar panel and 4 accumulators, we can see that one solar panel will produce 17.6 MJ of energy per day.
Due to rounding, this could be anywhere between 17.55 MJ and 17.65 MJ, therefore the experiment can be repeated over multiple days.
| day number | accumulator charge | energy produced per day |
|---|---|---|
| 1 | 17.6 MJ | 17.6 MJ |
| 2 | 35.3 MJ | 17.65 MJ |
| 3 | 52.9 MJ | 17.633 MJ |
| 4 | 70.6 MJ | 17.65 MJ |
| 5 | 88.2 MJ | 17.64 MJ |
| 6 | 106 MJ | 17.666 MJ |
Further experiments show that the true number will swing around and approach 17.64 MJ
A day on Nauvis lasts 7 minutes, or , which means that each solar panel provides about 42 kW of power on average.
Solarpanel output as a function
For further calculations we assume the power output function of a solar panel looks as follows:
Knowing how much power a solar panel provides on average we can construct a fitting load to test how much max accumulator charge is needed.
In a second experiment we take two solar panels on separate grids and put a load of on one, and one with , which can be achieved with...
- 8 Assembly machines 2 (5 kW per unit), and
- 3/4 fast inserters (500 W per unit), and
- 1/0 regular inserters (400 W per unit).
To that we add a generous 100 accumulators and observe the energy in the system.
Experimental values for the 41.9 kW grid show the first peak has a height of about 4.24 MJ, with each consecutive peak growing higher as the true output of a solar panel is indeed more than 41.9 kW.
Experimental values for the 42 kW grid show each peak reaching about 4.24 MJ, but falling short for 5 seconds if it has to start from no charge at all. This may be due to the fact that machines start to behave differently when power is low. However, if we start the experiment with some slight pre-existing charge, the system will be stable.
Accumulators per solar panel
4.24 MJ is enough to fill 0.848 accumulators as they can hold a charge of 5 MJ each. Conservatively we can therefore set 0.85 accumulators per solar panel, or a ratio of 20 solar panels to 17 accumulators. A less conservative approach is to use 0.84 accumulators per solar panel, or a ratio of 25 solar panels to 21 accumulators.
Analytic solution: 2646/3125
We can set the previously defined power function as the rate of change of the accumulator and subtract it's average output as the load which the setup should be able to continuously supply. First we check when the power reaches 42 kW
Then we shift the function for power in time and reduce it by the 42 kW so that the function will start at zero.
To find the critical point in time at which the accumulator charge reaches it's peak , we need to see when it's derivative passes zero. This happens in it's 3rd section.
The true perfect ratio for solar panels to accumulators therefore turns out to be...
It takes 0.84672 accumulators per solar panel, or a ratio of 2646 accumulators to 3125 solar panels. Speaking conservatively we can take a higher ratio of 0.85 with 17 accumulators to 20 solar panels.
Best ratios
These ratios approach the one we got from the analytic solution, but to get more accurate, they need a larger number of individual equipment to do so.
| accumulators | solar panels | ratio |
|---|---|---|
| 1 | 1 | 1 |
| 6 | 7 | 0.857142857 |
| 17 | 20 | 0.85 |
| 28 | 33 | 0.848484848 |
| 39 | 46 | 0.847826087 |
| 50 | 59 | 0.847457627 |
| 61 | 72 | 0.847222222 |
| 72 | 85 | 0.847058824 |
| 83 | 98 | 0.846938776 |
| 94 | 111 | 0.846846847 |
| 105 | 124 | 0.846774194 |
| 221 | 261 | 0.846743295 |
| 337 | 398 | 0.846733668 |
| 453 | 535 | 0.846728972 |
| 569 | 672 | 0.84672619 |
| 685 | 809 | 0.846724351 |
| 801 | 946 | 0.846723044 |
| 917 | 1083 | 0.846722068 |
| 1033 | 1220 | 0.846721311 |
| 1149 | 1357 | 0.846720707 |
| 1265 | 1494 | 0.846720214 |
| 2646 | 3125 | 0.84672 |
| accumulators | solar panels | ratio |
|---|---|---|
| 1 | 2 | 0.5 |
| 2 | 3 | 0.666666667 |
| 3 | 4 | 0.75 |
| 4 | 5 | 0.8 |
| 5 | 6 | 0.833333333 |
| 11 | 13 | 0.846153846 |
| 116 | 137 | 0.846715328 |
| 1381 | 1631 | 0.846719804 |
| 2646 | 3125 | 0.84672 |
Testing ratios
The most commonly recommended ratio is 21/25 or 0.84, let's see how it fairs against 17/20 or 0.84, and then check out ratios for 0.8467 and 0.8469. And for fairness, these tests start off with fully charged accumulators before a load is applied.
The tests support the analytic solution. The ratio for 0.8467 barely falls short of being able to sustain 42 kW of power, while 0.8469 almost fully discharges to 0.025%.