Tutorial:Applied power math: Difference between revisions
Lottery248 (talk | contribs) m →Quiz: modified second bonus question as the steam engine produces 900kW instead of 510kW as of version 0.15 |
m →Quiz |
||
| (11 intermediate revisions by 6 users not shown) | |||
| Line 6: | Line 6: | ||
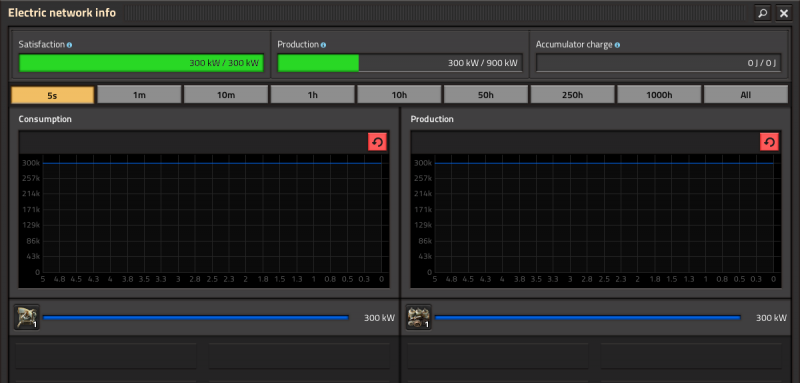
[[File:power-details.png|800px]] | [[File:power-details.png|800px]] | ||
Here we see one radar using | Here we see one radar using 300 kW of electrical power <math>P</math>. Factorio uses real science here. The unit of power, or energy transfer, is measured in Watt (W). A kilowatt (kW) is 1000 W, a megawatt (MW) is 1000 kW, and if you're lucky enough to ever make a factory big enough, a gigawatt (GW) is 1000 MW. | ||
So that answers the question of how much power our factory uses. To keep our factory running at full speed we need to maintain 300 kW. For ease of comparison, we'll convert that to 0.3 MW. | So that answers the question of how much power our factory uses. To keep our factory running at full speed we need to maintain 300 kW. For ease of comparison, we'll convert that to 0.3 MW. | ||
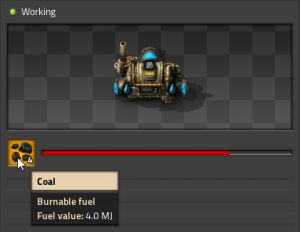
Next question! How much | Next question! How much energy <math>E</math> is released when burning one piece of coal? That's also easy, because it tells us when we hover over it: 4 MJ. | ||
[[File:coal-joules.png|300px]] | [[File:coal-joules.png|300px]] | ||
A Joule is | A Joule is the standard measure of energy <math>E</math>. As with Watts a kilojoule (kJ) is 1000 J, and so on. There is a fixed relationship between Joules and Watts. '''1 Joule of energy can provide 1 Watt of power for 1 second of time.''' So one Joule is equal to one Wattsecond. | ||
As a formula: | |||
<math> | |||
\begin{align} | |||
E &= P \cdot t\\ | |||
\left[ \text{J} \right] &= \left[ \text{W} \right] \cdot \left[ \text{s} \right] | |||
\end{align} | |||
</math> | |||
So to run our factory at 0.3 MW, we need to consume 0.3 MJ every second. | So to run our factory at 0.3 MW, we need to consume 0.3 MJ every second. | ||
| Line 22: | Line 28: | ||
== Quiz == | == Quiz == | ||
How long could one piece of coal <math>E = 4 \, \text{MJ}</math> run | |||
our single radar | our single radar <math>P = 0.3 \, \text{MW}</math>? | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
'''Expand to reveal answer''' | '''Expand to reveal answer''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math> | |||
\begin{align} | |||
J &= P \cdot t \\ | |||
t &= \frac{J}{P} \\ | |||
&= \frac{4 \, \text{MJ}}{0.3 \, \text{MW}} | |||
= \frac{4\,000\,000 \, \text{J}}{300\,000 \, \text{W}} | |||
= 13.333 \text{s} | |||
\end{align} | |||
</math> | |||
A bit more than 13 seconds. | |||
</div> | </div> | ||
</div> | </div> | ||
What is the maximum size factory (in watts) | |||
a single piece of coal could run for 5 | a single piece of coal <math>E = 4 \text{MJ} </math> could run for <math>t = 5 \text{s}</math>? | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
'''Expand to reveal answer''' | '''Expand to reveal answer''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math> | |||
\begin{align} | |||
J &= P \cdot t \\ | |||
P &= \frac{J}{t} \\ | |||
&= \frac{4 \, \text{MJ}}{5 \, \text{s}} | |||
= \frac{4\,000\,000 \, \text{J}}{5 \, \text{s}} | |||
= 800\,000 \, \text{W} | |||
= 0.8 \, \text{MW}\\ | |||
\end{align} | |||
</math> | |||
0.8 megawatts. | |||
</div> | </div> | ||
</div> | </div> | ||
'''BONUS!''' A ton of real world coal [http://hypertextbook.com/facts/2006/LunChen.shtml | '''BONUS!''' A metric ton of real world coal <math>m = 1 \, \text{ton}</math> can [http://hypertextbook.com/facts/2006/LunChen.shtml produce about 7.2 GJ in an electrical power plant]. How much does a piece of Factorio coal weigh? | ||
piece of Factorio coal weigh? | |||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| Line 58: | Line 77: | ||
The energy ratios will match the weight ratios, so: | The energy ratios will match the weight ratios, so: | ||
<math> | |||
\begin{align} | |||
\frac{m_\text{Factorio}}{m_\text{real}} = \frac{E_\text{Factorio}}{E_\text{real}} \quad \Leftrightarrow \quad | |||
m_\text{Factorio} &= \frac{E_\text{Factorio} \cdot m_\text{real}}{E_\text{real}} \\ | |||
1 \, \text{unit} &= \frac{4 \, \text{MJ}\cdot 1 \, \text{ton}}{7.2 \, \text{GJ}}\\ | |||
&= \frac{4\,000\,000 \, \text{J}\cdot 1\,000 \,\text{kg}}{7\,200\,000\,000 \, \text{J}}\\ | |||
&= 0.555\,555 \, \text{kg}\\ | |||
&= 555.555 \, \text{g}\\ | |||
\end{align} | |||
</math> | |||
About | About 555g! Still doesn't explain how our character can carry so much of it... | ||
</div> | </div> | ||
</div> | </div> | ||
Now we have everything we need to answer our initial question: '''how much coal do we need to power our factory?''' Well, the question actually needs to be a bit more precise: how much coal do we need ''per second'' to power our factory? | |||
<div class="toccolours mw-collapsible mw-collapsed"> | |||
'''Aside: why did the radar run for 20s and not 13.5s (50% of 27s)?''' | |||
<div class="mw-collapsible-content"> | |||
Because it doesn't turn on and off instantly<!--. As you can see in the graph -->, the radar's demand of electrical power ramps up before reaching its operating power demand, therefore its electrical power usage is a function of time <math>p_\text{el}(t)</math>. When speaking of a machine using power over time, the common equation symbol is <math>W</math> for '''performed work''', which must be equal to the amount of '''energy supplied''' <math>E_{supply}</math>. To easier visualize the amount of energy or work, in the real world, instead of Joule, the unit in use is the kilowatt-hour (kWh). | |||
<math>E_{supply} = W = \int p_\text{el}(t) \mathop{}\!\mathrm{d} t</math> | |||
However, as the accuracy of integration is not required, to conservatively approximate the required power supply the equation can be simplified by treating the average power <math>\bar{P}_\text{el}</math> as the radars peak operating power <math>\hat{P}_\text{el}</math> within a duration <math>T</math> as a constant. | |||
<math> | |||
\begin{align} | |||
E_{supply} &= \int_{t_0}^{t_0 + T} \hat{P}_\text{el}(t) \mathop{}\!\mathrm{d}t | |||
&= \hat{P}_\text{el} \cdot T | |||
\end{align} | |||
</math> | |||
For completeness sake it should be mentioned that the boilers turn 4 MJ of '''chemical energy''' <math>E_\text{chem}</math> stored in coal, to 4 MJ of '''thermal energy''' <math>E_\text{therm}</math> stored in the steam, which steam turbines only consume as the grid demands '''electrical energy''' <math>E_\text{el}</math>, where the grid then transfers '''electrical power per second'''. | |||
</div> | </div> | ||
</div> | </div> | ||
| Line 101: | Line 122: | ||
'''Expand to reveal answer''' | '''Expand to reveal answer''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
Since < | Since <math>E = P \cdot t</code>, a 20 MW factory will consume 20 MJ/s. Since coal contains 4 MJ, we'll need '''5 coal per second'''. | ||
<math> | |||
5 \cdot 4\, \text{MJ} = 20 \, \text{MW} | |||
</math> | |||
</div> | </div> | ||
</div> | </div> | ||
| Line 110: | Line 136: | ||
'''Expand to reveal answer''' | '''Expand to reveal answer''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
Per the linked page, an electric mining drill | Per the linked page, an electric mining drill mine 0.5 coal per second, so we'll need '''10 electric mining drills'''. | ||
<math>\frac{5 \, \text{units}}{\text{s}}{0.5\, \frac{\text{units}}{\text{s}}} = 5</math>. | |||
</div> | </div> | ||
</div> | </div> | ||
'''SECOND BONUS!''' The average American household uses [https://www.eia.gov/tools/faqs/faq.php?id=97&t=3 3.2 GJ in a month] (typically expressed as ''888 kilowatt hours''). How much Factorio coal would be needed to power one of these homes for that period, and how many homes could a steam engine support ([[Steam_engine|900 kW]]), assuming the power is used at a constant rate? (Assume 30 days in a month.) | '''SECOND BONUS!''' The average American household uses [https://www.eia.gov/tools/faqs/faq.php?id=97&t=3 3.2 GJ in a month] (typically expressed as ''888 kilowatt-hours''). How much Factorio coal would be needed to power one of these homes for that period, and how many homes could a steam engine support ([[Steam_engine|900 kW]]), assuming the power is used at a constant rate? (Assume 30 days in a month.) | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
'''Expand to reveal answer''' | '''Expand to reveal answer''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<math> | |||
\begin{align} | |||
3.2 \, \mathrm{GJ} &= 3\,200 \, \mathrm{MJ}\\ | |||
\frac{3\,200 \, \mathrm{MJ}}{4 \, \mathrm{MJ}} &= 800\\ | |||
\\ | |||
3\,200 \, \mathrm{MJ} &\cdot \frac{1 \, \mathrm{m}}{30 \, \mathrm{d}} \cdot \frac{1 \, \mathrm{d}}{24 \, \mathrm{h}} \cdot \frac{1 \, \mathrm{h}}{60 \, \mathrm{min}} \cdot \frac{1 \, \mathrm{min}}{60 \, \mathrm{s}} = 1\,234.567\,9 \, \mathrm{W}\\ | |||
\frac{900 \, \mathrm{kW}}{1\,234.567\,9 \, \mathrm{W}} &= 729 | |||
\end{align} | |||
</math> | |||
800 pieces of coal per household and a single steam engine could power 729 households exactly. | |||
800 pieces of coal per household | |||
</div> | </div> | ||
</div> | </div> | ||
Revision as of 08:53, 11 November 2024
In this tutorial we'll be answering the question: how much coal is needed to power a factory?
First off, we need to know: how much power does our factory use? That's easy - you can check the electricity tab by clicking on a power pole.
Here we see one radar using 300 kW of electrical power . Factorio uses real science here. The unit of power, or energy transfer, is measured in Watt (W). A kilowatt (kW) is 1000 W, a megawatt (MW) is 1000 kW, and if you're lucky enough to ever make a factory big enough, a gigawatt (GW) is 1000 MW.
So that answers the question of how much power our factory uses. To keep our factory running at full speed we need to maintain 300 kW. For ease of comparison, we'll convert that to 0.3 MW.
Next question! How much energy is released when burning one piece of coal? That's also easy, because it tells us when we hover over it: 4 MJ.
A Joule is the standard measure of energy . As with Watts a kilojoule (kJ) is 1000 J, and so on. There is a fixed relationship between Joules and Watts. 1 Joule of energy can provide 1 Watt of power for 1 second of time. So one Joule is equal to one Wattsecond. As a formula:
So to run our factory at 0.3 MW, we need to consume 0.3 MJ every second.
Quiz
How long could one piece of coal run our single radar ?
Expand to reveal answer
A bit more than 13 seconds.
What is the maximum size factory (in watts) a single piece of coal could run for ?
Expand to reveal answer
0.8 megawatts.
BONUS! A metric ton of real world coal can produce about 7.2 GJ in an electrical power plant. How much does a piece of Factorio coal weigh?
Expand to reveal answer
The energy ratios will match the weight ratios, so:
About 555g! Still doesn't explain how our character can carry so much of it...
Now we have everything we need to answer our initial question: how much coal do we need to power our factory? Well, the question actually needs to be a bit more precise: how much coal do we need per second to power our factory?
Aside: why did the radar run for 20s and not 13.5s (50% of 27s)?
Because it doesn't turn on and off instantly, the radar's demand of electrical power ramps up before reaching its operating power demand, therefore its electrical power usage is a function of time . When speaking of a machine using power over time, the common equation symbol is for performed work, which must be equal to the amount of energy supplied . To easier visualize the amount of energy or work, in the real world, instead of Joule, the unit in use is the kilowatt-hour (kWh).
However, as the accuracy of integration is not required, to conservatively approximate the required power supply the equation can be simplified by treating the average power as the radars peak operating power within a duration as a constant.
For completeness sake it should be mentioned that the boilers turn 4 MJ of chemical energy stored in coal, to 4 MJ of thermal energy stored in the steam, which steam turbines only consume as the grid demands electrical energy , where the grid then transfers electrical power per second.
Quiz
How much coal per second is needed to power a 20 MW factory?
Expand to reveal answer
Since
BONUS! How many mining drills are needed to produce that much coal?
Expand to reveal answer
Per the linked page, an electric mining drill mine 0.5 coal per second, so we'll need 10 electric mining drills.
.
SECOND BONUS! The average American household uses 3.2 GJ in a month (typically expressed as 888 kilowatt-hours). How much Factorio coal would be needed to power one of these homes for that period, and how many homes could a steam engine support (900 kW), assuming the power is used at a constant rate? (Assume 30 days in a month.)
Expand to reveal answer
800 pieces of coal per household and a single steam engine could power 729 households exactly.