教程:太阳能数学
在本教程中,我们将正确计算工厂所需的太阳能板和蓄电器的数量,以及这两种设施之间的适当比例。
方程中的符号和单位
本游戏使用国际单位制,并反映了它们在现实世界中的使用方式。能量 和 功率 通常可以互换使用,但功率是能量的一阶导数,即功率是每秒使用/产生的能量的值。通过调节功率,可以控制机器运行并使其做功 。做功的一个典型例子是克服重力加速度,将一定质量的物体抬升一定高度。一般来说,由于热能的耗散,可用的能量总会有损失,但游戏中并不考虑这种损失。最后是蓄电器的电量,其常用单位为库仑。现实中电容器中储存的电量取决于电荷量及其两端的电压,但由于游戏中并未涉及不同电压的问题,因此对于游戏中的蓄电器,其蓄电量 可以定义为与能量类似的综合值。
以下列出在方程中使用的重要能量符号:
- ... 能量,其单位为焦耳 ,另一个常用单位是千瓦时 ,
- ... 功,其单位为 或牛米 ,等价于焦耳
- ... 蓄电器电量,单位为焦耳
以及与功率相关的重要方程符号,其中时间导数以点标识:
- ... 供应的功率,其单位为瓦特 ,等价于焦耳每秒
- ... 机器运行所做的功,其单位为瓦特
- ... 蓄电器的充放电率,其单位为瓦特
根据能量守恒定律,能量不会凭空产生或消灭,只会在不同的形式间转化,即能量的变化率必然为0。因此,如果我们用供电功率减去机器运行的功率和蓄电器的充电功率(从电网中获取能量),其结果必然为0。所以有:
.
玩家通常无需担心过量发电的问题,因为任何发电设备都可以根据负荷自动调节其输出功率。只有在供电不足时,机器才会由于无法获得足够的电量而减缓其运行速度。因此在几乎所有情况下,这些比率都会随时间变化,太阳能板的发电量会随着一天中的时间变化而变化,而机器则会随其运行情况相应地增减电力消耗。例如,机械臂仅在搬运物品时才会消耗电力,而在待机状态下其功耗会小很多。有鉴于此,我们引入统计相关值的方程:
- 时间段 中的平均功率 以上划线标识:
- 峰值功率 以顶部箭头标识:
每片太阳能板的平均发电量
我们目前已经知道太阳能板的峰值发电功率为 ,但其精确的输出功率会随着一天中光照强度的变化而变化。幸运的是,我们可以使用蓄电器实现削峰填谷的功能,替我们进行积分计算:
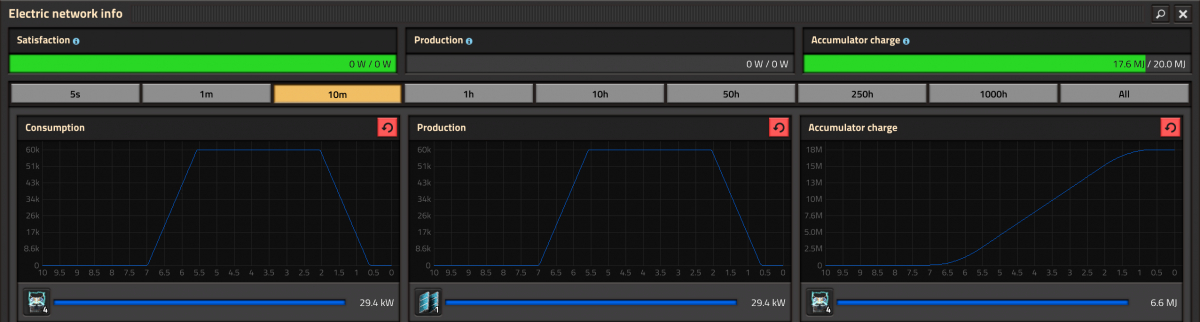
在由1片太阳能板和4台蓄电器构成的实验环境中,我们可以看到一片太阳能板每天的总发电量为 17.6 MJ。
由于四舍五入,精确的发电量数值可能在 17.55 MJ 至 17.65 MJ之间,因此这个实验可以在多日内重复进行。
| 天数 | 蓄电器充电量 | 每日发电量 |
|---|---|---|
| 1 | 17.6 MJ | 17.6 MJ |
| 2 | 35.3 MJ | 17.65 MJ |
| 3 | 52.9 MJ | 17.633 MJ |
| 4 | 70.6 MJ | 17.65 MJ |
| 5 | 88.2 MJ | 17.64 MJ |
| 6 | 106 MJ | 17.666 MJ |
进一步实验表明,实际的发电量数值会在 17.64 MJ 附近波动
在新地星,一天的时长为现实中的7分钟,即 ,这意味着每片太阳能板的平均发电量为 42 kW。
太阳能板发电功率函数
为进行进一步计算,我们定义太阳能板的输出功率函数如下:
在确定了太阳能板的平均发电量之后,我们就可以构建一个合适的负载模型来测试所需的最大蓄电器充电量 。
在第二个实验中,我们将两片太阳能板置于不同的电网中,为其中一个配置 的用电负荷,为另一个配置 的用电负荷,可能的组合包括...
- 8台 组装机2型 (每台 5 kW),和
- 3/4台 高速机械臂 (每台 500 W),和
- 1/0台 电力机械臂 (每台 400 W)。
在此基础上再添加100台蓄电器,并观察系统中的能量变化:
41.9 kW 电网的实验值显示,第一个峰值的数值约为 4.24 MJ,随着太阳能板的实际输出功率超过 41.9 kW,每个连续的峰值都越来越高。
42 kW 电网的实验值显示,每个峰值的数值约为 4.24 MJ,但如果完全从无电状态冷启动,则会在5秒内出现供电不足的情况。这可能是因为在低电量情况下开始实验时机器的表现有所不同。然而,如果我们在有少量预存电量的情况下开始实验,则系统将会是稳定的。
每片太阳能板所需的蓄电器数量
由于每台蓄电器的蓄电量为 5 MJ,因此 4.24 MJ 的能量可以充满 0.848 台蓄电器。据此我们可以保守设定每片太阳能板为0.85台蓄电器充电,即20片太阳能板对应17台蓄电器的比例。更加激进的方案是每片太阳能板为0.84台蓄电器充电,即25片太阳能板对应21台蓄电器的比例。
解析解:2646/3125
我们可以将先前定义的功率函数变形为蓄电器的充电速率,并将其平均输出功率作为该系统可以持续承受的负载。首先,我们检查负荷为 42 kW 的情况:
然后,我们对功率函数进行时间平移,并减去 42 kW 的基准值,使其从零开始。
为了计算出蓄电器的充电速率达到峰值 的临界时间 ,我们需要查看其导数何时过零。这通常在第3段发生。
因此,太阳能板与蓄电器的最佳比例结果是...
即每片太阳能板需要 0.84672 台蓄电器,或 2646 台蓄电器配置 3125 片太阳能板。保险起见,我们可以采用更高的比例,即每 20 片太阳能板配置 17 台蓄电器。
最佳比例
上述比例接近我们通过解析解得到的结果,但若要进一步提升精度,则需要更多数量的设施来实现。
| 蓄电器数量 | 太阳能板数量 | 比例 |
|---|---|---|
| 1 | 1 | 1 |
| 6 | 7 | 0.857142857 |
| 17 | 20 | 0.85 |
| 28 | 33 | 0.848484848 |
| 39 | 46 | 0.847826087 |
| 50 | 59 | 0.847457627 |
| 61 | 72 | 0.847222222 |
| 72 | 85 | 0.847058824 |
| 83 | 98 | 0.846938776 |
| 94 | 111 | 0.846846847 |
| 105 | 124 | 0.846774194 |
| 221 | 261 | 0.846743295 |
| 337 | 398 | 0.846733668 |
| 453 | 535 | 0.846728972 |
| 569 | 672 | 0.84672619 |
| 685 | 809 | 0.846724351 |
| 801 | 946 | 0.846723044 |
| 917 | 1083 | 0.846722068 |
| 1033 | 1220 | 0.846721311 |
| 1149 | 1357 | 0.846720707 |
| 1265 | 1494 | 0.846720214 |
| 2646 | 3125 | 0.84672 |
| 蓄电器数量 | 太阳能板数量 | 比例 |
|---|---|---|
| 1 | 2 | 0.5 |
| 2 | 3 | 0.666666667 |
| 3 | 4 | 0.75 |
| 4 | 5 | 0.8 |
| 5 | 6 | 0.833333333 |
| 11 | 13 | 0.846153846 |
| 116 | 137 | 0.846715328 |
| 1381 | 1631 | 0.846719804 |
| 2646 | 3125 | 0.84672 |
测试比例
实用的推荐比例是 21/25 或 0.84,接下来我们将考察它与 17/20 或 0.84 的比例,以及 0.8467 和 0.8469 的比例相比表现如何。为了公平起见,在测试开始前系统中的蓄电器均已完全充满。
测试结果符合解析解。0.8467 的比例略低于维持 42 kW 的需求,而 0.8469 的比例仅剩余 0.025% 的电量。