Tutorial:Combinator tutorial
Introduction
Combinator logic is achieved by cross-connecting outputs to inputs in such a way to achieve the desired logic. While advanced logic requires a multitude of combinators, some very useful basic logic can be achieved using only a handful of combinators. Combinator logic works because Factorio only updates at 60 times per second, such that combinators analyze their logic in a step, and then sum and/or decide the resulting output values on the next step.
When logic values are computed by combinators, the outputs are not recognized by the circuit network until the following step. So when a decider combinator is used to detect a certain input condition, it's output value will not take effect on the circuit network until the next step. This behavior is important to remember and can result in sequencing errors and significant delays when multiple combinators are connected in series.
Circuit wires act like a wire bus in electronics, it carries information in the connected wires, meaning that if there are similar signals on a wire, it will add them automatically, unless if it is a different signal, that means it will be carried in that wire as well, but as a different signal.
When cross-connecting combinators it's good practice to use the unused color to cross-connect, this will split the input and output networks and prevent unwanted inputs from accidentally connecting to a larger circuit network. Combinators will sum the red & green inputs prior to calculation, so either color can be used when wiring the output back to the input, but in most cases, it is more useful to use the opposing colour of the wire so that it will not interfere with the resulting output and input.
There is also an example heavy circuit network cookbook that you may find helpful to learn and refer to about circuit networks.
Input Isolator & Gate
An arithmetic combinator set to (In: Each + 0, Out: Each) can be used to swap wire colors and as an isolator to prevent downstream logic from backfeeding into the circuit network's inputs.
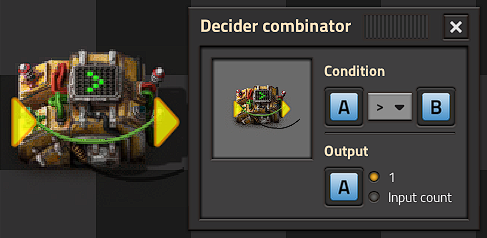
A decider combinator set to (Out: Everything, Input-> Output) will also function as an isolator as long as the set logic condition is true. This can also selectively pass or 'gate' inputs only when desired. This could be used to sequentially poll remote train stations for their chest contents, and include only desired stations.
Set/Reset Latching Switch
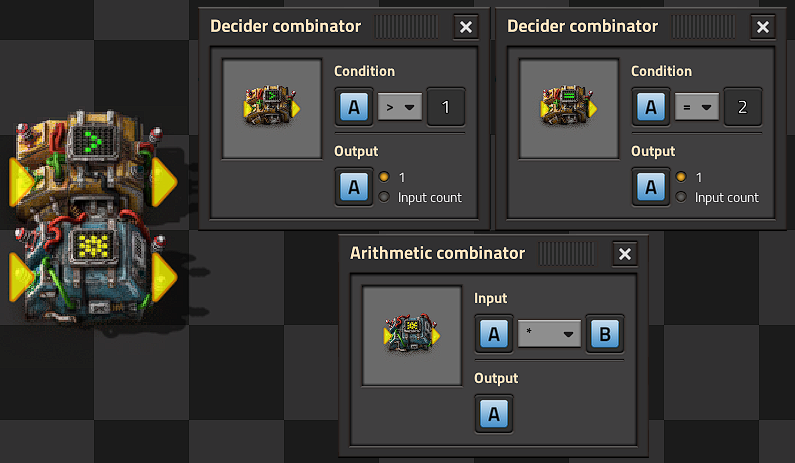
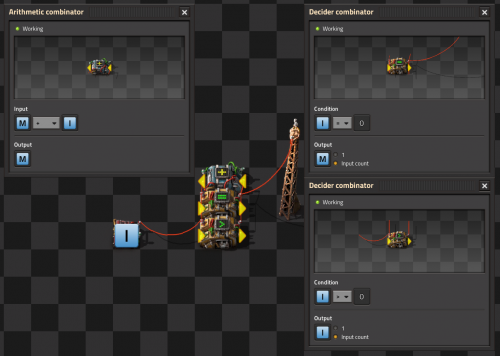
You want something to SET a trigger at some quantity, but then STAY on until that quantity hits some other value, the RESET value. You'll need one decider combinator and one arithmetic combinator. Two decider combinators and a constant combinator can also be used for more complex multi-channel conditions.
Setup the first decider combinator to the desired set conditional and to output a 1. Then connect the output to the input of an arithmetic combinator, and configure it to multiply by the bias value, the difference between the set and reset values, and wire the arithmetic output to the input of the decider. The arithmetic output channel MUST be set the same as the decider's input channel. That's it! Whenever your set conditional is reached, the decider will output a '1', and the bias of the arithmetic combinator will be applied. This will 'hold' the output true until the value goes back below the reset point.
Here's a more specific example :
i want the pump to run when petrol reach 2000, and turn off when reach 200.
only with green wire
Tank -> in decider
out decider-> in arithmetic
out arithmetic -> in decider
green wire from in decider, to pump
Pump have the same condition as the decider (Petrol > 2000)
Decider : Petrol > 2000
out : A = 1
Arithmetic : A x 1800 (2000 - 200 )
out : petrol
File:Factorio combinator switch.png
Comparing Outputs
Addressing Outposts
Smart Train Loading
Intially designed by MadZuri,
This solves the problem of loading logistics into chests, which tend to be unequal and is slower in the rate of loading logistics into the cargo of trains.
To setup the design, you require an Arithmetic Combinator, as well as Red and Green wires. Wire all the chests used, to the input of the Arithmetic Combinator. Then write (Logistics Item / -Amount of chests) and as the output as the Logistics Item in the Arithmetic Combinator, this will average the amount of items within the chests. Lastly, wire all the inserters used to the output of the Arithmetic Combinator and have the other color of the wire be wired to the adjacent chest. Have the inserters enabled when Logistics Item < 1.
A more visual representation as well as questions for the design can be found here.
Explanation of why this works: It compares the average amount of total items within the chests and the chest adjacent to the inserter so that it activates when the average number of items is higher than the amount within the chest. The reason for why the division denominator is negative is because if the items in the chests are 0, it basically makes it so that it adds 1 to the equation.
Oil Control
Memory
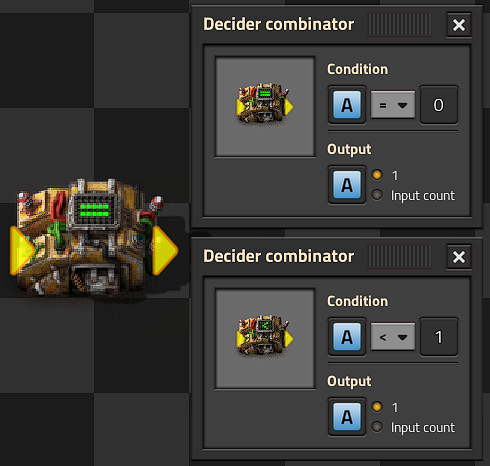
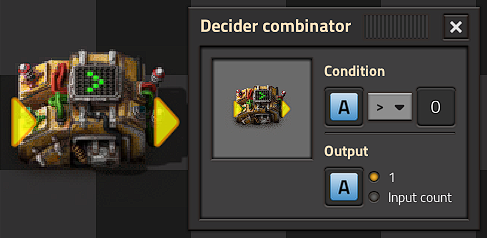
How to store a constant value for later use, either for a basic counter or for more advanced logic. A decider combinator wired output tied to input and configured greater than zero (for positive values), input -> output will 'hold' a value, as long as all other inputs on the network are zero.
Any non-zero input condition will create a basic clock; incrementing the stored value by the sum of all connected input values every cycle. A single pulse of an input will cause a single increment by the pulsed value. Reset to zero occurs whenever the set condition is no longer met, or if a negative pulse equal to the input occurs.
Basic Clocks
Clocks are constructed by having the output of a combinator tied back to its own input, such that every cycle advances its own count. Either the arithmetic combinator or the decider combinator can be used.
An arithmetic combinator tied to itself is fun to watch and will happily run-away, but requires additional control logic to reset.
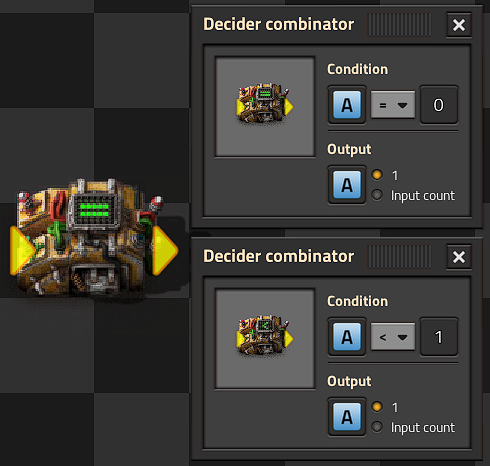
A self-resetting clock requires just a single decider combinator with output wired to input and configured with Less Than (<) and Input -> Output. When a constant combinator is then connected to the input, every cycle it will count up by the value of the Constant Combinator until the set conditional value is reached, then output a zero which will be summed with the constant combinator, and reset the process.
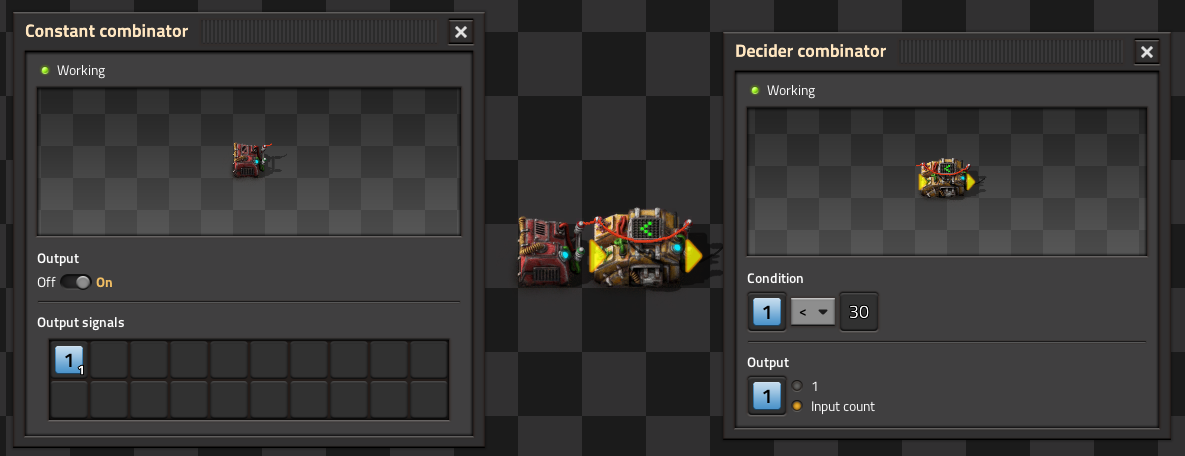Signal 0 is the ceiling for Signal 1; which is continuously added.
The clock sequence will not include zero, will begin at the value set by the constant combinator, and will include whatever value eventually causes the conditional to be false. An arithmetic combinator can modify the clock sequence but remember its outputs will occur one cycle later than the clock cycle values.
Pulse Generators
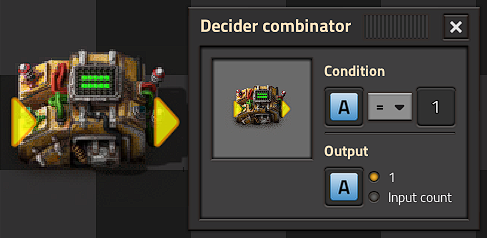
Connecting an additional (=) decider combinator to the output of a basic clock will create a pulse generator, and will pulse a single output every time the clock cycles through the set condition. Any output value can be used, either directly from the clock sequence (input->output), a 1, or some value on a separate logic channel on the circuit network, such as set by a constant combinator. or by the circuit network.
The value 0 can be written as any positive integer, so long as it is within the cap of your timer.
Counter
A counter is used to count the number of input events, and output the sum of that count. Any pulsing input into a decider combinator configured input -> output and wired between output and input will create a counter, but this input must be zero at all other times or else the combinator will run away like a clock. A pulse generator is normally used to accomplish this. Combining several gating decider isolators set with sequential conditionals, a clock, and a pulse generator to the input of a counter will allow remote polling and counting of each isolator's contents.
Logic Gates
A, B represents inputs. A' (A Prime) represents the 2nd A input, A* (A Star) represents the 3rd A input.
Unary NOT
Truth Table:
A | A (Output) 0 | 1 1 | 0
Binary OR
Truth Table:
A | A' | A (Output) 0 | 0 | 0 0 | 1 | 1 1 | 0 | 1 1 | 1 | 1
Binary NOR
Truth Table:
A | A' | A (Output) 0 | 0 | 1 0 | 1 | 0 1 | 0 | 0 1 | 1 | 0
Binary XOR
Truth Table:
A | A' | A (Output) 0 | 0 | 0 0 | 1 | 1 1 | 0 | 1 1 | 1 | 0
Binary AND
Truth Table:
A | A'/ B | A (Output) 0 | 0 | 0 0 | 1 | 0 1 | 0 | 0 1 | 1 | 1
Trinary AND
Truth Table:
A | A' | A* | A (Output) 0 | 0 | 0 | 0 0 | 1 | 0 | 0 1 | 0 | 0 | 0 0 | 0 | 1 | 0 0 | 1 | 1 | 0 1 | 0 | 1 | 0 1 | 1 | 1 | 1
Binary NAND
Truth Table:
A | A' | A (Output) 0 | 0 | 1 0 | 1 | 1 1 | 0 | 1 1 | 1 | 0
Binary XNOR/XAND
Truth Table:
A | A' | A (Output) 0 | 0 | 1 0 | 1 | 0 1 | 0 | 0 1 | 1 | 1
Memory Cells
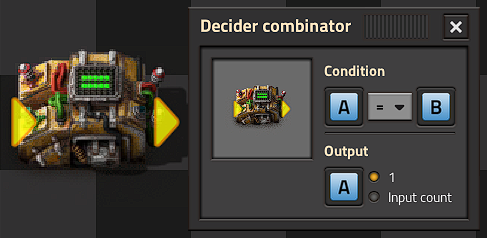
Simple Latch
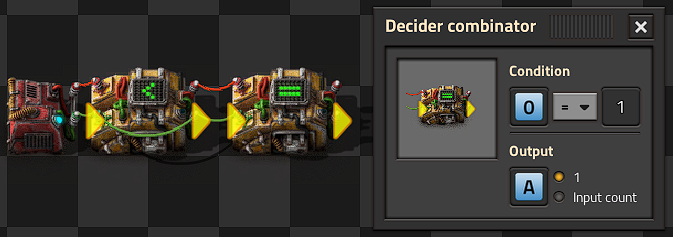
Have a Decider Combinator connect to itself with its input and output using a different colour of wire, say green wire when your output and input is red wire.
Truth Table:
A'| A | B | A' (t+1) 0 | 0 | 0 | 0 0 | 1 | 0 | 1 0 | 0 | 1 | 0 0 | 1 | 1 | 0 1 | 0 | 0 | 1 1 | 1 | 0 | 1 (2) 1 | 0 | 1 | 0 1 | 1 | 1 | 1 (2)
A' is the green wire seen in the picture, it carries A.
Binary Cell
RS NOR Latch File:RS-NOR.png
Advanced Cell
Cell for storing a positive value:
Connect the desired value as signal 3 on the right side to set the memory cell and connect a negative value as signal 3 to reset the cell.
Address Enable Switch