User:Fluffyliberta

Precise Mathematical Analysis

To determine the exact number of centrifuges required for maintaining reactor stability without using the Kovarex enrichment process, we need to employ probability theory. This analysis will help us estimate the probability of obtaining the required amount of uranium-235 and the number of centrifuges needed.

The primary goal of these calculations is to derive a formula that can be easily applied and sustainable for predictions despite advancements in technologies, game version updates, or in-game developments and modifications.

Variables

Let's introduce some variables that we'll need in further calculations

• T - overall time of a reactor working (in seconds*)
• t - time of a reactor cycle (in seconds*)
• c - consumption of uranium-235 per reactor cycle
• k - centrifuges number (our target value for calculations)
• p - probability of uranium-235 production per centrifuge cycle
• n - overall number of centrifuge cycles
• τ - centrifuge time per cycle to produce 1 recipe
• α - desired probability of having success number uranium-235 to sustain all T time of reactor stable work**

* Measured in seconds or in-game ticks, this does not affect the general reasoning

** Known as the [confidence level]. Due to the nature of probability, this value can only be in the interval (0; 1). We will use the values 0.9, 0.95, and 0.99 to maintain scientific rigor and ease of interpretation, opposite to the [significance level].

Assumptions

Assumption 1

All k centrifuges work continuously and simultaneously for each n cycle with the same τ

Assumption 2

There are always enough resources to convert uranium-235 into reactor fuel *

Assumption 3

The conversion of uranium-235 into fuel for reactors can be neglected **

Assumption 4 (for long-term play)

The game can be played indefinitely (technically assumed for practical use, average playtime suffices)

* For instance, base game uranium-238 has a very high probability (0.993), ensuring a sufficient supply for uranium fuel cell production.

** For instance, converting base game uranium-235 into 10 uranium fuel cells takes 12 sec, but the reactor cycle is 200 sec - a negligible time difference, easily managed by building more assemblers.

Exact Approach (Short-run)

The main question we aim to answer:

How many k centrifuges are needed during n cycles of centrifuge production to sustain a reactor working continuously for T time with probability α?

Assume each centrifuge in each production cycle is represented by a discrete random variable X_ij, where i is the centrifuge number and j is the production cycle number. If X_ij produces uranium-235, its value is Xij=1. If not, Xij=0. Thus, P(Xij = 1) = 0.007 and P(Xij = 0) = 0.993 (This is a [Bernoulli distribution]).

To find out how long centrifuges should produce uranium-235 to sustain a reactor: From one side, the reactor has T/t working cycles, needing a total of Tc/t uranium-235 to run continuously for time T. Let's denote this value as u: u=Tc/t. From the other side, the centrifuges work continuously for n cycles during time T: T = n*τ.

Combining these, our required quantity of u is u=n*τ*c/t for the entire reactor operation time T.

Consider the simple case where we need n cycles and k centrifuges to produce exactly u uranium-235 (technically, we need ceil of u, but it won't be practically useful and doesn't detract generality of our calculations). Each X_ij is a Bernoulli trial, so Xall = ∑in∑jkXij is the total production, distributed as a [binomial distribution] Xall ~ B(nk, p). This gives the probability of producing exactly u uranium-235 in n cycles with k centrifuges:

P(Xall=u) = Cnku * pu * (1-p)nk-u

Practically, we are interested in producing at least u uranium-235, corresponding to P(Xall ≥ u). This can be calculated as P(Xall ≥ u) = 1 - P(Xall < u), where P(Xall < u) is the [cumulative distribution function]:

P(Xall≥u) ≥ α ⇒ 1 - ∑mu-1P(Xall=m) ≥ α ⇒ {using results from paragraph 1} ⇒ ∑mn*τ*c/t-1Cnkm * pm * (1-p)nk-m ≤ 1 - α

So, we now have a formula to determine the number of k centrifuges needed to sustain a reactor with consumption c during n cycles. This formula is general and not always practical for long-term play due to the high values of n and u. It is best suited for short-term or speedrun calculations.

Example Base Game Short-Term

To illustrate, let's determine how many centrifuges are needed to sustain 1 reactor with 0.99 confidence without modules. It's a common mistake to think that 0.007 is the production speed, but it represents the probability of producing uranium-235 per cycle. Suppose we want a reactor to work for 2000 centrifuge production cycles (about 6.7 hours of reactor operation) with 1 centrifuge:

n	tau	c	t	m	p	u	ceil(u-1)	alpha	1-alpha		k	C(nk, m)	P(m)	∑mP
2000	12	0,1	200	0	0,007	12	11	0,99	0,01		1	1	7,92E-07	7,92E-07
2000	12	0,1	200	1	0,007	12	11	0,99	0,01		1	2000	1,12E-05	1,20E-05
2000	12	0,1	200	2	0,007	12	11	0,99	0,01		1	2,0E+06	7,86E-05	9,06E-05
2000	12	0,1	200	3	0,007	12	11	0,99	0,01		1	1,3E+09	0,0004	0,0005
2000	12	0,1	200	4	0,007	12	11	0,99	0,01		1	6,6E+11	0,0013	0,0018
2000	12	0,1	200	5	0,007	12	11	0,99	0,01		1	2,7E+14	0,0037	0,0054
2000	12	0,1	200	6	0,007	12	11	0,99	0,01		1	8,8E+16	0,0086	0,0140
2000	12	0,1	200	7	0,007	12	11	0,99	0,01		1	2,5E+19	0,0172	0,0312
2000	12	0,1	200	8	0,007	12	11	0,99	0,01		1	6,3E+21	0,0302	0,0302
2000	12	0,1	200	9	0,007	12	11	0,99	0,01		1	1,4E+24	0,0472	0,0472
2000	12	0,1	200	10	0,007	12	11	0,99	0,01		1	2,8E+26	0,0662	0,1133
2000	12	0,1	200	11	0,007	12	11	0,99	0,01		1	5,0E+28	0,0844	0,1977
2000	12	0,1	200	12	0,007	12	11	0,99	0,01		1	8,3E+30	0,0986
2000	12	0,1	200	13	0,007	12	11	0,99	0,01		1	1,3E+33	0,1063

As you can see, we need to produce 12 u for 2000 cycles. According to our formula, we need to sum up all the probabilities of producing less than 12 uranium-235 and compare this with our desired confidence level:

∑m2000120.1/200-1C20001m * 0.007m * (1-0.007)20001-m = 7.92E-07 + 1.12E-05 + 7.86E-05 + 0.0004 + 0.0013 + 0.0037 + 0.0086 + 0.0172 + 0.0302 + 0.0472 + 0.0662 + 0.0844 = 0.1977

We can interpret this value as the "Probability of producing less than the required amount of uranium-235 for 2000 centrifuge cycles." This probability should be less than 1-α = 0.01. However, since it is not, we cannot be sure that 1 centrifuge will produce enough uranium-235 to sustain reactor operation during 2000 cycles. Therefore, we need to increase the number of centrifuges.

n	tau	c	t	m	p	u	ceil(u-1)	alpha	1-alpha		k	C(nk, m)	P(x=m)	sum(P(m<=ceil(u-1)))
2000	12	0,1	200	0	0,007	12	11	0,99	0,01		2	1	6,3E-13	6,27E-13
2000	12	0,1	200	1	0,007	12	11	0,99	0,01		2	4000	1,8E-11	1,83E-11
2000	12	0,1	200	2	0,007	12	11	0,99	0,01		2	8,0E+06	2,5E-10	2,67E-10
2000	12	0,1	200	3	0,007	12	11	0,99	0,01		2	1,1E+10	2,3E-09	2,61E-09
2000	12	0,1	200	4	0,007	12	11	0,99	0,01		2	1,1E+13	1,6E-08	1,91E-08
2000	12	0,1	200	5	0,007	12	11	0,99	0,01		2	8,5E+15	9,3E-08	1,12E-07
2000	12	0,1	200	6	0,007	12	11	0,99	0,01		2	5,7E+18	4,4E-07	5,48E-07
2000	12	0,1	200	7	0,007	12	11	0,99	0,01		2	3,2E+21	1,8E-06	2,30E-06
2000	12	0,1	200	8	0,007	12	11	0,99	0,01		2	1,6E+24	6,2E-06	6,17E-06
2000	12	0,1	200	9	0,007	12	11	0,99	0,01		2	7,2E+26	1,9E-05	1,93E-05
2000	12	0,1	200	10	0,007	12	11	0,99	0,01		2	2,9E+29	0,0001	0,0001
2000	12	0,1	200	11	0,007	12	11	0,99	0,01		2	1,0E+32	0,0001	0,0002
2000	12	0,1	200	12	0,007	12	11	0,99	0,01		2	3,4E+34	0,0003
2000	12	0,1	200	13	0,007	12	11	0,99	0,01		2	1,1E+37	0,0007

And now you can see that our condition is fulfilled. Therefore, we can say that without any modules or Kovarex enrichment process, we can achieve the stability of 1 reactor during 2000 centrifuge cycles using at least 2 centrifuges! However, does this imply that we need 4 centrifuges for 2 reactors, 6 centrifuges for 3 reactors, and so on? I encourage you to think about this question yourself. You may be surprised by the results when applying the approach outlined above.

Distribution Approximation (Medium-run)

If you plan to play for an extended period while your reactor setup is operating, we can consider n→∞. In this case, since our centrifuges' overall production Xall ~ B(nk, p), we can use the [De Moivre-Laplace theorem]. In short, it states that if our random variable follows a binomial distribution with a large number of trials, then (Xall-nkp)/sqrt(nkp(1-p)) ~ N(0, 1). Thus, to estimate P(Xall ≥ u), we simplify it to:

P((Xall-nkp)/sqrt(nkp(1-p))) ≥ (u-nkp)/sqrt(nkp(1-p)) ≥ α ⇒ {1-Pdist ≥ α} ⇒ (nkp - u)/sqrt(nkp(1-p)) ≥ ɸ-1(1-α), where ɸ^-1 is the inverse standard normal distribution, found using the [standard normal table].

Let's denote ɸ-1(α) as λ. For each confidence level α, we can calculate it from the standard normal table: λ0.99=2.3263, λ0.95=1.6449, λ0.9=1.2816.

Now we need to solve the equation above for the variable k:

(nkp-u)/sqrt(nkp(1-p)) ≥ λ ⇒ (nkp-nτc/t)/sqrt(nkp(1-p)) ≥ λ.

After some basic arithmetic operations and solving the quadratic equation, you can determine the value of k:

k ≥ [(χ1 + sqrt(χ12 + 4χ0χ2))/(2*χ0)]2 where χ0 = np, χ1 = λ*sqrt(np(1-p)), χ2 = nτc/t, λ is the inverse standard normal distribution (popular values: 2.3263; 1.6449; 1.2816 for corresponding α values: 0.99; 0.95; 0.9).

This formula can be calculated for very large n. That's why it's best choice for planning average playtime of experienced player.

Infinite Approximation (Long-run)

If we consider the formula for k centrifuges above, we can derive an analytical form for n→∞ by substituting all χ into the formula and finding the limit:

limn→∞(χ1 + sqrt(χ12 + 4χ0χ2))/(2*χ0) ⇒ {substitute all χ} ⇒ k ≥ τ*c/(p*t)

Thus, to determine the minimal number of centrifuges needed to achieve reactor stability, we use the final formula:

k = ⌈τ*c/(p*t)⌉, where ⌈x⌉ is the ceiling function

Notice that this formula does not depend on λ. This is because, as n approaches infinity, the cumulative probability tends to 1. In other words, with an infinite number of cycles, we can be 100% certain that this number of centrifuges will sustain our reactor's stability indefinitely.

This formula provides the minimal number of centrifuges needed to sustain reactor stability indefinitely. To determine this number, we need only 4 parameters.

Conclusion

Through detailed probability calculations and binomial distribution analysis, we have determined the number of centrifuges required to sustain a reactor's operation. The key findings are:

• Minimum Centrifuges for Reactor Stability: Without any modules or the Kovarex enrichment process, a minimum of 2 centrifuges are needed to ensure the continuous operation of a single reactor over 2000 cycles with a confidence level of 0.99. However, be careful about using such result for extending it on 2, 3, 4 and more reactors, as it will be enough, but not optimal quantity.

• General Formula for Long-Term Play: For an infinite number of cycles, the formula k = ⌈τ * c / (p * t)⌉ provides the minimal number of centrifuges required to sustain reactor stability indefinitely. This formula is derived from the behavior of the binomial distribution as the number of cycles approaches infinity. The derived formula for the infinite approximation does not depend on the confidence interval parameter λ and cycles n, making it robust and straightforward to apply for long-term game planning.

• As these results are based on using abstract recipe cycle of centrifuges, it doesn't depend on in-game ticks implementation and real time estimation.

• Probability estimation for short-term of centrifuges produce desired amount of uranium-235.

• We derived 2 important formulas:

Medium-term

k = ⌈[(χ1 + sqrt(χ12 + 4χ0χ2))/(2*χ0)]2⌉

where χ0 = np, χ1 = λ*sqrt(np(1-p)), χ2 = nτc/t, λ is the inverse standard normal distribution

Long-term

k = ⌈τ*c/(p*t)⌉

• Rule of thumb: If you need to quickly estimate how many centrifuges are required to initiate and maintain the stability of reactors in the medium term (over the next few hours), just build an additional 1/3 of the long-term value. From Example 2, you can use the golden ratio and build 1.15 centrifuges per reactor to ensure stability.

Usage examples

Example 1

2 methods convergence comparison (example 1)

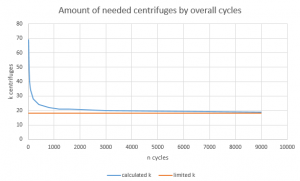
Let's find out how many centrifuges do you need for playing long-run playtime and average playtime for 20 reactors without any modules and kovarex enrichment process.

First of all, notice that we can pretend that 20 reactors are just one big reactor and the only parameter that will be influenced is c. As we have 20 times more reactors, that means that our default consumption will be 20 times more, then we have c = 20*0.1 = 2. So now we can use 2 methods for long-run and medium-run estimations:

Long-run doesn't depend on n that's why we can easily calculate it: k=⌈τ*c/(p*t)⌉=18.

Medium-run has explicit formula, but need to iterate over n. I've built a graph to explicitly show, that after many centrifuges cycles, medium-run amount of k tends to Long-run amount. If we take 1000 cycles and 0.99 confident level, then k = 22. On the other side, 1000 cycles is equal to 3.33 hours. This is the main reason why you need understand importance of both estimations. As after setting centrifuge configuration by long-term value, you won't be stable after 3.3 hours and there can be shortages in uranium-235 production.

Example 2 (Golden ratio)

Assume that the reactor's consumption depends only on the total number of reactors and consider a long-term play scenario. In the base game, we know that each reactor consumes 1/10 of a unit of uranium-235 per reactor cycle.

This leads us to c = 0.1 * R, where R is the number of reactors. Using the long-term formula, we can derive the optimal centrifuge to reactor ratio:

k / R = τ / (10 * p * t)

If you are playing without modules, the value is: 12 / (10 * 0.007 * 200) = 0.8571. So, if you have 4 reactors, you will need at least 4 centrifuges for long-term stability.