User:Ndh: Difference between revisions
| Line 14: | Line 14: | ||
Note that constant combinators can also produce negative values, which will decrease the stored value in the example below. If the decider combinator uses > 0 as the condition, only positive values will be allowed, so the value will stop decreasing if 0 is reached. If the condition is ≠ 0, negative values will also be allowed. | Note that constant combinators can also produce negative values, which will decrease the stored value in the example below. If the decider combinator uses > 0 as the condition, only positive values will be allowed, so the value will stop decreasing if 0 is reached. If the condition is ≠ 0, negative values will also be allowed. | ||
A single pulse of an input will cause a single increment by the pulsed value, creating a counter. Reset to zero occurs if a negative pulse equal to the input occurs. | A single pulse of an input will cause a single increment by the pulsed value, creating a counter. In the following blueprint, place one item on the belt. Every time it is scanned by the connected belt, a pulse is generated that increments the stored value. | ||
{{BlueprintString|bp-string=0eNqllMGO4jAMQP/F5zAqpaXQw/7IahWljQFLbVIlLtoK5d83aXdZEJ3DMBeQU+fFenZyg6YbcXBkGOobUGuNh/rnDTydjerSGk8DQg3E2IMAo/oUsVPGD9bxpsGOIQggo/E31NvwSwAaJiZcSHMwSTP2DbqY8BlDwGB93GZNOjWiqqL8KAVMUG/KQ/ZRhiBeaPl7tG2kCdDksF1S8hX27gvs/XOlT+xCQNTKznaywYu6knVpX0uuHYklGtV0KDX59A/1SXUexf2zQ6XlRRktEySWGK2yGx8y/q0vqb3VEZKF+VCz1ODTedv0c3aI5rEtpKEu/7NSGFsY1lwX7/l4cV2ssMs7W2NLGt2mtX1DRnGUtcI/fmo7X7f9F5tkabo7OZHzLF9m/UqOx7hyL2rJ2OAV3cQXMmdY/HpW6eJkKegH5eZya/gRd9qRh/Eb7GGKtY6G5cnZXpKJsKXx4Sut3T24Xml1HlstIP/uZOzfuoXVcf1OV2/N2Ux7moR9eormZ6t+eOUERNF+GZXDtqiOeXXYH7NdVoTwB9igtjA=}} | |||
Reset to zero occurs if a negative pulse equal to the input occurs. | |||
== Basic clocks == | == Basic clocks == | ||
Revision as of 18:09, 27 June 2024
Basic memory
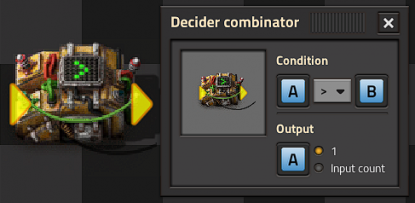
A decider combinator can be used to store values, either for a counter or for more advanced logic (see below). The decider combinator is configured with
- input and output connected to the same network (typically each other),
- condition set to a signal > 0 for positive values or ≠ 0 to store both positive and negative values,
- output set to the input signal or [*].
As long as all inputs on the network are zero, it will hold the previously set value, because the game will copy the input to the output every tick.
A non-zero input held over time, e. g. the output of a constant combinator, will create a basic runaway clock. The stored value will be incremented by the sum of all connected input values every cycle. So e. g. with a constant combinator that produces [A]=10 connected to the memory, the network will store the value 10 in the first pulse, 20 in the second, incrementing 60 times per second.
Typically a constant combinator producing 1 will be used.
Note that constant combinators can also produce negative values, which will decrease the stored value in the example below. If the decider combinator uses > 0 as the condition, only positive values will be allowed, so the value will stop decreasing if 0 is reached. If the condition is ≠ 0, negative values will also be allowed.
A single pulse of an input will cause a single increment by the pulsed value, creating a counter. In the following blueprint, place one item on the belt. Every time it is scanned by the connected belt, a pulse is generated that increments the stored value.
Reset to zero occurs if a negative pulse equal to the input occurs.
Basic clocks
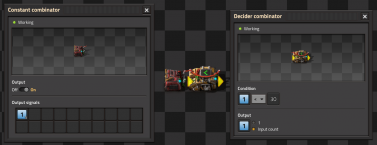
Clocks are constructed by having the output of a combinator tied back to its own input, such that every cycle advances its own count. Either the arithmetic combinator or the decider combinator can be used.
An arithmetic combinator tied to itself is fun to watch and will happily run-away, but requires additional control logic to reset.
A self-resetting clock requires just a single decider combinator with output wired to input and configured with Less Than (<) and Input -> Output. When a constant combinator is then connected to the input, every cycle it will count up by the value of the Constant Combinator until the set conditional value is reached, then output a zero which will be summed with the constant combinator, and reset the process.
The clock sequence will not include zero, will begin at the value set by the constant combinator, and will include whatever value eventually causes the conditional to be false. An arithmetic combinator can modify the clock sequence but remember its outputs will occur one cycle later than the clock cycle values.
A clock that only counts once can be built using the following setup:
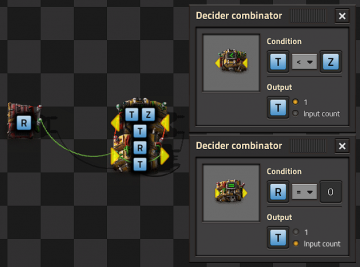
Pulse generators
Connecting an additional (=) decider combinator to the output of a basic clock will create a pulse generator, and will pulse a single output every time the clock cycles through the set condition. Any output value can be used, either directly from the clock sequence (input->output), a 1, or some value on a separate logic channel on the circuit network, such as set by a constant combinator. or by the circuit network.
- The value 1 can be written as any positive integer, so long as it is within the cap or ceiling of your timer.
- As an example from the above timer, this light will pulse every 1st tick after the timer reaches 30 ticks, making it pulse 1/30th of a second, as Factorio updates at 60 times per second.
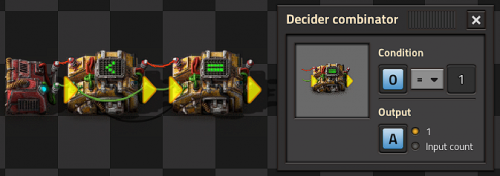
Counter
A counter is used to count the number of input events, and output the sum of that count. Any pulsing input into a decider combinator configured input -> output and wired between output and input will create a counter, but this input must be zero at all other times or else the combinator will run away like a clock. A pulse generator is normally used to accomplish this. Combining several gating decider isolators set with sequential conditionals, a clock, and a pulse generator to the input of a counter will allow remote polling and counting of each isolator's contents.
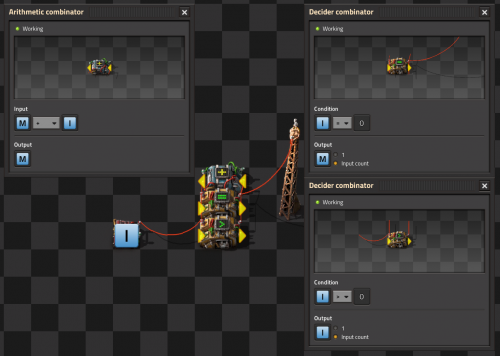
Memory cells
Simple latch
When looping the combinator to itself, use a different color of wire from your main inputs or outputs.
Truth Table:
| Output 1 | Input 1 | Input 2 | Output 1 (t+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 (2) |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 (2) |
Output 1 is the green wire loop seen in the picture, it carries the value to latch.
Input 1 is Set, while Input 2 is Reset.
Positive cell
Cell for storing a positive value, with reset support:
Connect the desired value as signal I on the right side to set the memory cell and connect a negative value as signal I to reset the cell.
- The output of the memory cell is 2 mutually exclusive signals.
- In case input signal I > 0 then signal I is passed to the other side.
- In case input signal I is interrupted, then signal M is passed instead as a memory of previous input value.
- When input signal I is interrupted, it takes 2 ticks to switch to memory signal M.
- In case input I signal lasts only one tick then memory cell starts to cycle between the 2 previous values, tick by tick. Indefinitely.
- Switching is seamless, e.g. there are no ticks with empty signal.
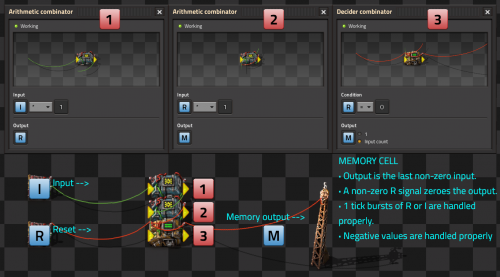
Positives and negatives cell
This cell can store negatives or positives. Reset is done on a dedicated line. Additionally, a 1-tick burst is handled properly. Forum post.
- The output M (memory) is the last non-zero input I (Input).
- A non zero R (reset) signal sets the output to zero.
- 1-tick bursts of R or I are handled properly.
- Negatives are handled properly.
Multiplier and Dictionaries/Arrays
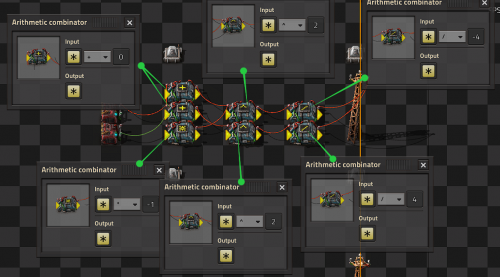
- Multiplying two signals together is simple and requires only a single combinator, however multiplying a set of signals is more complicated.
- A proof is shown below for the equation and why it works.
- A dictionary is a system that allows a value on a specific signal to be accessed. For example, A can contain many signals (either from a constant combinator or memory cell) and B can contain 1 of a specific signal (such as blue signal). What remains is the blue-signal value from A. This is because all the other signals are multiplied by 0.
- Arrays are similar to dictionaries, but instead of using a signal as a key, we use a number. Constant combinators are placed mapping each signal to a unique number (such as 1 yellow belt, 2 red belt, 3 blue belt, 4 burner inserter, etc). Then, use a combinator of "each = index OUTPUT 1 of each" and plug that in as the input to a dictionary.

((A+B)^2 - (A-B)^2)/4 = AB (A+B)^2 - (A-B)^2 = 4AB (A^2 + 2AB + B^2) - (A^2 - 2AB + B^2) = 4AB 4AB = 4AB