Power production: Difference between revisions
m (→Ensuring enough energy is produced: dont link to unrelated wikipedia page for brownout/blackout) |
(→Solar panels and accumulators: Add some Vulcanus data and forum links) |
||
| (31 intermediate revisions by 12 users not shown) | |||
| Line 3: | Line 3: | ||
== Steam engine power == | == Steam engine power == | ||
Each [[steam engine]] needs 0.5 [[boiler]]s when running at full capacity. One [[offshore pump]] can supply | Each [[steam engine]] needs 0.5 [[boiler]]s when running at full capacity. One [[offshore pump]] can supply 200 boilers and 400 steam engines. | ||
The above ratio can be calculated from information available in-game: One boiler consumes 1.8MW of fuel and produces energy stored in steam at 100% efficiency. One steam engine consumes 900kW of energy stored in steam, so each boiler can supply 2 steam engines: < | The above ratio can be calculated from information available in-game: One boiler consumes 1.8MW of fuel and produces energy stored in [[steam]] at 100% efficiency. One steam engine consumes 900kW (0.9MW) of energy stored in steam, so each boiler can supply 2 steam engines: <math>\frac{1.8}{0.9} = 2</math>. One boiler consume 6 unit of [[water]] to produce 60 unit of [[steam]] per second, one steam engine consume 30 steam per second (3 units of water) and one offshore pump produces 1200 water per second, so each offshore pump produces enough water to supply 200 boilers: <math>\frac{1200}{6} = 200</math>. Two steam engines per boiler give us 400. This produces the 1:200:400 ratio. | ||
[[File:SteamSetupExample.png|center|600px|thumb|A possible setup]] | [[File:SteamSetupExample.png|center|600px|thumb|A possible setup.]] | ||
== Solar panels and accumulators == | == Solar panels and accumulators == | ||
| Line 15: | Line 15: | ||
The optimal ratio is 0.84 (21:25) [[accumulator]]s per [[solar panel]], and 23.8 solar panels per megawatt required by your factory (this ratio accounts for solar panels needed to charge the accumulators). This means that you need 1.428 MW of production (of solar panels) and 100MJ of storage to provide 1 MW of power over one day-night cycle. | The optimal ratio is 0.84 (21:25) [[accumulator]]s per [[solar panel]], and 23.8 solar panels per megawatt required by your factory (this ratio accounts for solar panels needed to charge the accumulators). This means that you need 1.428 MW of production (of solar panels) and 100MJ of storage to provide 1 MW of power over one day-night cycle. | ||
A "close enough" ratio is 20:24:1 accumulators to solar panels to megawatts required (for example, a factory requiring 10 MW can be approximately entirely powered, day and night, by 200 accumulators and 240 solar panels - this approximation differs from optimal only in that it calls for | A "close enough" ratio is 20:24:1 accumulators to solar panels to megawatts required (for example, a factory requiring 10 MW can be approximately entirely powered, day and night, by 200 accumulators and 240 solar panels - this approximation differs from optimal only in that it calls for 2 extra solar panels, which is negligible but remember that the difference between the "close enough" ratio and the optimal ratio increases as you add more solar panels). | ||
This is taken from [http://www.factorioforums.com/forum/viewtopic.php?f=5&t=5594 Accumulator / Solar Panel Ratio] (which calculates this in an impressive mathematical way!) and [https://forums.factorio.com/viewtopic.php?p=143317#p143317 another post in that thread] (which calculates the solar panel to megawatt ratio in a different way). | This is taken from [http://www.factorioforums.com/forum/viewtopic.php?f=5&t=5594 Accumulator / Solar Panel Ratio] (which calculates this in an impressive mathematical way!) and [https://forums.factorio.com/viewtopic.php?p=143317#p143317 another post in that thread] (which calculates the solar panel to megawatt ratio in a different way). | ||
[[File:9x9_accumulator_solar_panel_example.jpg|300px|thumb|top|A small 9x9 setup demonstrating the 20:24 "close enough" ratio above.]] | [[File:9x9_accumulator_solar_panel_example.jpg|300px|thumb|top|A small 9x9 setup demonstrating the 20:24 "close enough" ratio above.]] | ||
=== Calculations === | === Calculations === | ||
The optimal ratio of accumulators per solar panel relies on many values in the game. These include the power generation of a solar panel, the energy storage of an accumulator, the length of a [[day]], and the length of a night. There are also times between day and night called dusk and dawn which complicate the calculations. In vanilla factorio, without mods which change any of these values, the optimal ratio will be the same. This ratio is | The optimal ratio of accumulators per solar panel relies on many values in the game. These include the power generation of a solar panel, the energy storage of an accumulator, the length of a [[Time#Days|day]], and the length of a night. There are also times between day and night called dusk and dawn which complicate the calculations. In vanilla factorio, without mods which change any of these values, the optimal ratio will be the same. This ratio is | ||
< | |||
<math> \frac{\mathrm{Accumulators}}{\mathrm{SolarPanels}} = \frac{\left( \mathrm{day} + \mathrm{dawn} \right)}{\mathrm{gameday}} \cdot \left( \mathrm{night} + \frac{\mathrm{dawn} \cdot \left( \mathrm{day} + \mathrm{dawn} \right)}{\mathrm{gameday}} \right) \cdot \frac{\mathrm{SolarPower}}{\mathrm{AccumulatorEnergy}} </math> | |||
which, given the default time lengths of: day = 12500/60 s; dawn or dusk = 5000/60 s; night = 2500/60 s, and the default: Solar_power = 60 kW; Accumulator_energy = 5 MJ = 5000 kJ, gives the optimal ratio of 0.84 accumulators per solar panel. If the player uses mods which change the power generation of solar panels, or the energy storage of accumulators, but <b>not</b> the length of days, a simplified version of this equation can be used. | which, given the default time lengths of: day = 12500/60 s; dawn or dusk = 5000/60 s; night = 2500/60 s, and the default: Solar_power = 60 kW; Accumulator_energy = 5 MJ = 5000 kJ, gives the optimal ratio of 0.84 accumulators per solar panel. If the player uses mods which change the power generation of solar panels, or the energy storage of accumulators, but <b>not</b> the length of days, a simplified version of this equation can be used. | ||
| Line 33: | Line 33: | ||
where game_day is the number of seconds in the game day which is 25000/60 s by default. | where game_day is the number of seconds in the game day which is 25000/60 s by default. | ||
=== Vulcanus === | |||
In Space Age, the day/night cycle on Vulcanus is 90 seconds with each phase of that cycle proportionally smaller: day = 45 s; dawn or dusk = 18 s; night = 9 s. The formula above simplifies to: | |||
<pre>Accumulators / Solar_panels = 15.2 s × Solar_power / Accumulator_energy</pre> | |||
Additionally, solar power production in Vulcanus atmosphere is 400% of that of Nauvis. With normal quality solar panels and accumulators, the ratio is 0.72576 accumulator per solar panel. 3 accumulators per 4 panel is pretty close. | |||
=== See also === | === See also === | ||
| Line 39: | Line 48: | ||
* [http://www.factorioforums.com/forum/viewtopic.php?f=18&t=5394 Solar ratios (Factorio forums)] | * [http://www.factorioforums.com/forum/viewtopic.php?f=18&t=5394 Solar ratios (Factorio forums)] | ||
* [http://www.factorioforums.com/forum/viewtopic.php?f=5&t=7619 1 solar panel produces 42KW after factoring in the night (Factorio forums)] | * [http://www.factorioforums.com/forum/viewtopic.php?f=5&t=7619 1 solar panel produces 42KW after factoring in the night (Factorio forums)] | ||
* [https://forums.factorio.com/viewtopic.php?p=629003#p629003 Day-Night cycle times in Space Age and Solar Power (Factorio forums)] | |||
* [https://forums.factorio.com/viewtopic.php?f=18&t=119040 Solar Power in Space Age - Definitive Ratios for Planets, Qualities and Throughput-Limits (Factorio forums)] | |||
== Nuclear power == | == Nuclear power == | ||
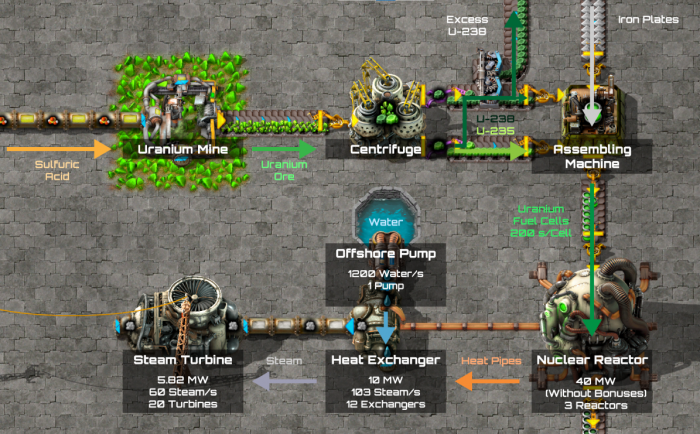
[[File:Nuclear setup.png|thumb|700px|right|Uranium processing for nuclear power.]] | |||
:''See also: [[Tutorial:Nuclear power]]'' | :''See also: [[Tutorial:Nuclear power]]'' | ||
In general, nuclear power is produced by the following production chain: [[Uranium ore]] is mined and [[Uranium processing|processed]] to [[uranium-235]] and [[uranium-238]], then [[uranium fuel cell]]s are created from the two. These fuel cells are then burned in a [[nuclear reactor]] to create heat. The heat can be used to convert [[water]] to [[steam]] using a [[heat exchanger]] and the steam can be consumed by [[steam turbine]]s to produce power. | In general, nuclear power is produced by the following production chain: [[Uranium ore]] is mined and [[Uranium processing|processed]] to [[uranium-235]] and [[uranium-238]], then [[uranium fuel cell]]s are created from the two. These fuel cells are then burned in a [[nuclear reactor]] to create heat. The heat can be used to convert [[water]] to [[steam]] using a [[heat exchanger]] and the steam can be consumed by [[steam turbine]]s to produce power. | ||
| Line 47: | Line 59: | ||
{| class="wikitable" | {| class="wikitable" | ||
! Ideal Ratio !! Simple Ratio !! Building | ! Ideal Ratio !! Simple Ratio !! Building | ||
|- | |- | ||
| | | 2 || 1 ||{{imagelink|Offshore pump}} | ||
|- | |- | ||
| | | 233 || 116(12) || {{imagelink|Heat exchanger}} | ||
|- | |- | ||
| | | 400 || 200(20) || {{imagelink|Steam turbine}} | ||
|} | |} | ||
== Heating tower {{SA}} == | |||
The [[Heating tower]], initially researched on [[Gleba]], is an alternate source of heat for [[Heat pipe]]s and [[Heat exchanger]]s. Unlike nuclear reactors, heating towers are traditional [[burner devices]], burning standard [[fuel]]s. | |||
Heating towers burn fuel, extracting 16MW of power from the fuel. However, because they have 250% efficiency, they generate 40MW of heat from the fuel. Like a nuclear reactor, the heat must be transferred to heat exchangers to generate useful electricity. Since they use the same fuel, but can produce 2.5x the energy from it, one can think of a heating tower as a [[boiler]] "Mk 2". | |||
A single heating tower can produce the same power output as a single nuclear reactor. However, they do not get neighbor bonuses the way reactors do. As such, the ratio of heating towers to exchangers is always 1:4. | |||
Like reactors, they have a maximum temperature of 1000 C. And also like reactors, they will continue to burn fuel even after they reach their maximum temperature. This gives them a secondary use as a quick way to dispose of unwanted burnable materials, such as excess fruit products/[[spoilage]] on Gleba or excess solid fuel on [[Fulgora]]. | |||
Note that heating towers produce more pollution per MW of power produced than boilers, even for the same energy output. This only matters for [[Nauvis]]; using heating towers for power, or even [[biter egg]] disposal, can draw [[Enemies]] to your base. | |||
== Lightning power{{SA}} == | |||
On Fulgora, when a [[lightning rod]] or [[lightning collector]] is struck by lightning, it becomes a short-lived source of electrical power. The way it works is as follows. | |||
A rod/collector has an energy capacity as well as an efficiency (the latter varies by [[quality]]). When a lightning bolt strikes, the energy stored in the rod/collector is charged by the percentage of its total energy capacity. A base quality rod has a capacity of 500 MJ and 20% efficiency, so a single bolt will charge the collector by 20% of 500 MJ, or 100 MJ. | |||
Rods/collectors have a discharge rate of 150 MW. When they have stored energy, they will discharge 150 MJ of their stored energy per second into the [[Electric system]] it is attached to. This will provide power to any buildings attached to it, as well as [[accumulator]]s. However, if the local electrical network cannot consume all 150 MW of power output, it will still be drained from the stored capacity. So lightning power is a "use it or lose it" arrangement. | |||
A base quality lightning rod struck by a single bolt will only generate 150 MW of power for 0.67 seconds. A base quality lightning collector will generate 150 MW for 2.67 seconds. The principle advantages of collectors is the larger range for lightning strikes and their longer discharge times. | |||
The key to taking advantage of this is to use accumulators, in large quantities. Each accumulator can only be charged by 0.3 MW (at base quality). Since rods/collectors discharge so much energy all at once, you need a lot of accumulators to capture it. It would require 500 accumulators to not waste any energy from a single lightning rod. However, this ratio is usually over-kill. If rods/collectors cover a large area, many of them will get struck through the night, allowing accumulators to reliably charge during the night at their full power. They can then discharge throughout the day. | |||
== Fusion power{{SA}} == | |||
Fusion power requires the production of two ingredients to function: [[fusion power cell]]s and [[fluoroketone (cold)]]. Both can only be produced on [[Aquilo]] using the planet's exclusive fluid resources, and [[holmium plate]]s imported from [[Fulgora]]. | |||
[[Fusion reactor]]s consume the power cells, cold fluoroketone, and electricity to produce [[plasma]]. The plasma is fed into [[fusion generator]]s which produce electricity and [[fluoroketone (hot)]]. The hot fluoroketone must then be fed into a [[cryogenic plant]] to cool it back down, which can produce an self-sustaining loop. However, as the reactors require electricity (10 mW) to generate plasma, there must be some other power source already on the network to jump-start the system. After that, even a single fusion generator will create enough power to sustain the reactor. | |||
Because the fluids which produce the power cells and hot fluoroketone cannot be [[barrel|barrelled]], production of them is confined to Aquilo. However, as the cold fluoroketone ''can'' be barreled, it and the power cells can be shipped to other planets with relative ease. | |||
=== Ratio calculations === | |||
Fusion reactors produce plasma at a base temperature of <math>1,M^\circ \text{C}</math>. Each directly connected reactor adds an additional <math>1,M^\circ \text{C}</math> to the maximum achievable plasma temperature. The actual plasma temperature depends on the neighbor bonuses, which are determined by the arrangement of reactors and their current plasma production rate. For example, if a reactor produces plasma at its maximum rate, all reactors connected to this reactor receive a 100% neighbor bonus. The temperature used by generators is the average plasma temperature of all reactors in the setup. | |||
The optimal ratio of fusion reactors to generators can be calculated in a single step: | |||
<math>G = (R + N) \cdot \frac{P_{O}}{P_{C}}</math> | |||
where: | |||
* <math>G</math> is the optimal number of fusion generators for the given reactor setup | |||
* <math>R</math> is the number of fusion reactors | |||
* <math>N</math> is the sum of the neighbor bonuses of all reactors (expressed as an integer) | |||
* <math>P_O</math> is the maximum plasma output of a reactor | |||
* <math>P_C</math> is the maximum plasma consumption of a generator | |||
Thus, the optimal reactor-to-generator ratio is <math>R:G</math> | |||
If the fusion reactors and generators have the same quality tier (e.g. normal), then the formula simplifies to: | |||
<math>G = 2 \cdot (R + N)</math> | |||
'''Note''': | |||
* This formula applies to all quality tiers and mixed setups where reactors and generators share the same quality tier respectively. | |||
* Initially, a not fully utilized fusion power setup will produce plasma at a lower temperature than what is possible. As more power is needed, more plasma is produced, and therefore the neighbor bonuses rise. With rising neighbor bonuses, the resulting plasma temperature also increases, resulting in more efficient plasma usage. This cycle continues until the setup reaches its maximum plasma temperature, allowing it to deliver peak power output. | |||
== Ensuring enough energy is produced == | == Ensuring enough energy is produced == | ||
| Line 69: | Line 140: | ||
See also the [[Tutorial:Applied_power_math|applied power math tutorial]] to answer the question ''how much coal do I need?'' | See also the [[Tutorial:Applied_power_math|applied power math tutorial]] to answer the question ''how much coal do I need?'' | ||
{{C|Production{{!}}#Power production}} {{C|Energy{{!}}#Power production}} | |||
Revision as of 09:32, 2 December 2024
Electricity has to be produced before it can be transferred to consumers over the electric system. There are multiple methods to produce electricity:
Steam engine power
Each steam engine needs 0.5 boilers when running at full capacity. One offshore pump can supply 200 boilers and 400 steam engines.
The above ratio can be calculated from information available in-game: One boiler consumes 1.8MW of fuel and produces energy stored in steam at 100% efficiency. One steam engine consumes 900kW (0.9MW) of energy stored in steam, so each boiler can supply 2 steam engines: . One boiler consume 6 unit of water to produce 60 unit of steam per second, one steam engine consume 30 steam per second (3 units of water) and one offshore pump produces 1200 water per second, so each offshore pump produces enough water to supply 200 boilers: . Two steam engines per boiler give us 400. This produces the 1:200:400 ratio.
Solar panels and accumulators
Optimal ratio
The optimal ratio is 0.84 (21:25) accumulators per solar panel, and 23.8 solar panels per megawatt required by your factory (this ratio accounts for solar panels needed to charge the accumulators). This means that you need 1.428 MW of production (of solar panels) and 100MJ of storage to provide 1 MW of power over one day-night cycle.
A "close enough" ratio is 20:24:1 accumulators to solar panels to megawatts required (for example, a factory requiring 10 MW can be approximately entirely powered, day and night, by 200 accumulators and 240 solar panels - this approximation differs from optimal only in that it calls for 2 extra solar panels, which is negligible but remember that the difference between the "close enough" ratio and the optimal ratio increases as you add more solar panels).
This is taken from Accumulator / Solar Panel Ratio (which calculates this in an impressive mathematical way!) and another post in that thread (which calculates the solar panel to megawatt ratio in a different way).
Calculations
The optimal ratio of accumulators per solar panel relies on many values in the game. These include the power generation of a solar panel, the energy storage of an accumulator, the length of a day, and the length of a night. There are also times between day and night called dusk and dawn which complicate the calculations. In vanilla factorio, without mods which change any of these values, the optimal ratio will be the same. This ratio is
which, given the default time lengths of: day = 12500/60 s; dawn or dusk = 5000/60 s; night = 2500/60 s, and the default: Solar_power = 60 kW; Accumulator_energy = 5 MJ = 5000 kJ, gives the optimal ratio of 0.84 accumulators per solar panel. If the player uses mods which change the power generation of solar panels, or the energy storage of accumulators, but not the length of days, a simplified version of this equation can be used.
Accumulators / Solar_panels = 70 s × Solar_power / Accumulator_energy
This equation could also be used to remember the vanilla optimal ratio given its simplicity. If the only effect the mod has on the game is it changes the total length of one day, without changing the ratio of dusk : day : dawn : night, then the equation can be simplified as
Accumulators / Solar_panels = 0.002016 /s × game_day
where game_day is the number of seconds in the game day which is 25000/60 s by default.
Vulcanus
In Space Age, the day/night cycle on Vulcanus is 90 seconds with each phase of that cycle proportionally smaller: day = 45 s; dawn or dusk = 18 s; night = 9 s. The formula above simplifies to:
Accumulators / Solar_panels = 15.2 s × Solar_power / Accumulator_energy
Additionally, solar power production in Vulcanus atmosphere is 400% of that of Nauvis. With normal quality solar panels and accumulators, the ratio is 0.72576 accumulator per solar panel. 3 accumulators per 4 panel is pretty close.
See also
- Perfectly optimal solar network (Factorio forums)
- Solar ratios (Factorio forums)
- 1 solar panel produces 42KW after factoring in the night (Factorio forums)
- Day-Night cycle times in Space Age and Solar Power (Factorio forums)
- Solar Power in Space Age - Definitive Ratios for Planets, Qualities and Throughput-Limits (Factorio forums)
Nuclear power
- See also: Tutorial:Nuclear power
In general, nuclear power is produced by the following production chain: Uranium ore is mined and processed to uranium-235 and uranium-238, then uranium fuel cells are created from the two. These fuel cells are then burned in a nuclear reactor to create heat. The heat can be used to convert water to steam using a heat exchanger and the steam can be consumed by steam turbines to produce power.
A reactor without neighbor bonus needs 4 heat exchangers so that all its heat gets consumed. For each 100% neighbor bonus, the reactor needs 4 more heat exchangers.
| Ideal Ratio | Simple Ratio | Building |
|---|---|---|
| 2 | 1 | Offshore pump |
| 233 | 116(12) | Heat exchanger |
| 400 | 200(20) | Steam turbine |
Heating tower 
The Heating tower, initially researched on Gleba, is an alternate source of heat for Heat pipes and Heat exchangers. Unlike nuclear reactors, heating towers are traditional burner devices, burning standard fuels.
Heating towers burn fuel, extracting 16MW of power from the fuel. However, because they have 250% efficiency, they generate 40MW of heat from the fuel. Like a nuclear reactor, the heat must be transferred to heat exchangers to generate useful electricity. Since they use the same fuel, but can produce 2.5x the energy from it, one can think of a heating tower as a boiler "Mk 2".
A single heating tower can produce the same power output as a single nuclear reactor. However, they do not get neighbor bonuses the way reactors do. As such, the ratio of heating towers to exchangers is always 1:4.
Like reactors, they have a maximum temperature of 1000 C. And also like reactors, they will continue to burn fuel even after they reach their maximum temperature. This gives them a secondary use as a quick way to dispose of unwanted burnable materials, such as excess fruit products/spoilage on Gleba or excess solid fuel on Fulgora.
Note that heating towers produce more pollution per MW of power produced than boilers, even for the same energy output. This only matters for Nauvis; using heating towers for power, or even biter egg disposal, can draw Enemies to your base.
Lightning power
On Fulgora, when a lightning rod or lightning collector is struck by lightning, it becomes a short-lived source of electrical power. The way it works is as follows.
A rod/collector has an energy capacity as well as an efficiency (the latter varies by quality). When a lightning bolt strikes, the energy stored in the rod/collector is charged by the percentage of its total energy capacity. A base quality rod has a capacity of 500 MJ and 20% efficiency, so a single bolt will charge the collector by 20% of 500 MJ, or 100 MJ.
Rods/collectors have a discharge rate of 150 MW. When they have stored energy, they will discharge 150 MJ of their stored energy per second into the Electric system it is attached to. This will provide power to any buildings attached to it, as well as accumulators. However, if the local electrical network cannot consume all 150 MW of power output, it will still be drained from the stored capacity. So lightning power is a "use it or lose it" arrangement.
A base quality lightning rod struck by a single bolt will only generate 150 MW of power for 0.67 seconds. A base quality lightning collector will generate 150 MW for 2.67 seconds. The principle advantages of collectors is the larger range for lightning strikes and their longer discharge times.
The key to taking advantage of this is to use accumulators, in large quantities. Each accumulator can only be charged by 0.3 MW (at base quality). Since rods/collectors discharge so much energy all at once, you need a lot of accumulators to capture it. It would require 500 accumulators to not waste any energy from a single lightning rod. However, this ratio is usually over-kill. If rods/collectors cover a large area, many of them will get struck through the night, allowing accumulators to reliably charge during the night at their full power. They can then discharge throughout the day.
Fusion power
Fusion power requires the production of two ingredients to function: fusion power cells and fluoroketone (cold). Both can only be produced on Aquilo using the planet's exclusive fluid resources, and holmium plates imported from Fulgora.
Fusion reactors consume the power cells, cold fluoroketone, and electricity to produce plasma. The plasma is fed into fusion generators which produce electricity and fluoroketone (hot). The hot fluoroketone must then be fed into a cryogenic plant to cool it back down, which can produce an self-sustaining loop. However, as the reactors require electricity (10 mW) to generate plasma, there must be some other power source already on the network to jump-start the system. After that, even a single fusion generator will create enough power to sustain the reactor.
Because the fluids which produce the power cells and hot fluoroketone cannot be barrelled, production of them is confined to Aquilo. However, as the cold fluoroketone can be barreled, it and the power cells can be shipped to other planets with relative ease.
Ratio calculations
Fusion reactors produce plasma at a base temperature of . Each directly connected reactor adds an additional to the maximum achievable plasma temperature. The actual plasma temperature depends on the neighbor bonuses, which are determined by the arrangement of reactors and their current plasma production rate. For example, if a reactor produces plasma at its maximum rate, all reactors connected to this reactor receive a 100% neighbor bonus. The temperature used by generators is the average plasma temperature of all reactors in the setup.
The optimal ratio of fusion reactors to generators can be calculated in a single step:
where:
- is the optimal number of fusion generators for the given reactor setup
- is the number of fusion reactors
- is the sum of the neighbor bonuses of all reactors (expressed as an integer)
- is the maximum plasma output of a reactor
- is the maximum plasma consumption of a generator
Thus, the optimal reactor-to-generator ratio is
If the fusion reactors and generators have the same quality tier (e.g. normal), then the formula simplifies to:
Note:
- This formula applies to all quality tiers and mixed setups where reactors and generators share the same quality tier respectively.
- Initially, a not fully utilized fusion power setup will produce plasma at a lower temperature than what is possible. As more power is needed, more plasma is produced, and therefore the neighbor bonuses rise. With rising neighbor bonuses, the resulting plasma temperature also increases, resulting in more efficient plasma usage. This cycle continues until the setup reaches its maximum plasma temperature, allowing it to deliver peak power output.
Ensuring enough energy is produced
Try this checklist before you completely revamp your power source. You may also use this to rectify brownouts/blackouts.
- Did you connect the steam engine to the electric system? If not, a small yellow triangle will flash. To fix, Add some power poles near the steam engines that go to machines needing that power. Any power pole will work.
- Is steam able to reach all steam engines?
- Do your pipes have water? Look at the windows in the pipes, hover over the pipes! Place some pipes or a tank at the end to see if there is really water coming through. If not, ensure all pipes or underground pipes are connected together.
- Is the factory producing enough fuel (coal, solid fuel, uranium fuel cells)?
- Are there enough steam generators (boilers, heat exchangers)?
- Are there enough steam engines/turbines?
See also the applied power math tutorial to answer the question how much coal do I need?